题目内容
已知α∈（0，π），sinα+cosα=
计算：
（1）sinαcosα
（2）sinα-cosα
| 1 |
| 3 |
（1）sinαcosα
（2）sinα-cosα
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：（1）把所给的等式平方，化简可得sinαcosα的值．
（2）由题意可得sinα＞0，cosα＜0，再根据sinα-cosα=
，计算求得结果．
（2）由题意可得sinα＞0，cosα＜0，再根据sinα-cosα=
| (sinα-cosα)2 |
解答：
解：（1）∵α∈（0，π），sinα+cosα=
，∴1+2sinαcosα=
，
∴sinαcosα=-
．
（2）由（1）sinαcosα＜0可得α为钝角，sinα＞0，cosα＜0，
∴sinα-cosα=
=
=
=
．
| 1 |
| 3 |
| 1 |
| 9 |
∴sinαcosα=-
| 4 |
| 9 |
（2）由（1）sinαcosα＜0可得α为钝角，sinα＞0，cosα＜0，
∴sinα-cosα=
| (sinα-cosα)2 |
| 1-2sinαcosα |
1+
|
| ||
| 3 |
点评：本题主要考查同角三角函数的基本关系、以及三角函数在各个象限中的符号，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
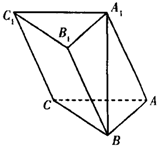如图，在三棱柱ABC-A1B1C1中，A1B⊥平面ABC，AB⊥AC．
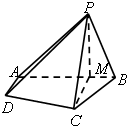在四棱锥P-ABCD中，AD∥BC，∠ABC=∠APB=90°，点M是线段AB上的一点，且PM⊥CD，AB=BC=2PB=2AD=4BM．