题目内容
已知集合A1={z|z
+3i（
-z）+5=0，z∈C}，集合A2={ω|ω=2iz，z∈A1}，当z1∈A1，z2∈A2时，求|z1-z2|的最大值与最小值．
. |
| z |
. |
| z |
考点：复数代数形式的混合运算
专题：数系的扩充和复数
分析：由复数的运算可得两集合均为圆上的点，由圆的几何知识可得．
解答：
解：设复数z=x+yi，其中x，y为实数，
根据z
+3i（
-z）+5=0可得x2+y2+3i（-2yi）+5=0
即x2+y2+6y+5=0，即x2+（y+3）2=4
A1表示以（0，-3）为圆心2为半径的圆上的点，
又w=2iz=-2y+2xi，设w=x′+y′i
则x′=-2y，y′=2x，即x=
，y=-
，
把x和y代入上述圆的方程可得y′2+x′2-12x′+20=0，
配方可得（x′-6）2+y′2=16，
也表示一个圆，圆心为（6，0）半径为4，
∴A2表示以（6，0）为圆心4为半径的圆上的点，
可得两圆心之间的距离为
=3
，
可得3
＞2+6，故两圆相离，
|z1-z2|表示两个圆上的点的距离，
显然最大值为圆心距加上两个半径和6+3
，
最小值为圆心距减掉两个半径和3
-6
根据z
. |
| z |
. |
| z |
即x2+y2+6y+5=0，即x2+（y+3）2=4
A1表示以（0，-3）为圆心2为半径的圆上的点，
又w=2iz=-2y+2xi，设w=x′+y′i
则x′=-2y，y′=2x，即x=
| y′ |
| 2 |
| x′ |
| 2 |
把x和y代入上述圆的方程可得y′2+x′2-12x′+20=0，
配方可得（x′-6）2+y′2=16，
也表示一个圆，圆心为（6，0）半径为4，
∴A2表示以（6，0）为圆心4为半径的圆上的点，
可得两圆心之间的距离为
| 62+(-3)2 |
| 5 |
可得3
| 5 |
|z1-z2|表示两个圆上的点的距离，
显然最大值为圆心距加上两个半径和6+3
| 5 |
最小值为圆心距减掉两个半径和3
| 5 |
点评：本题考查复数的代数形式的混合运算，涉及复数的几何意义，属中档题．
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
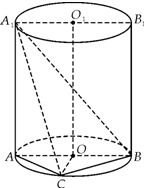如图，已知AB是圆柱OO1底面圆O的直径，底面半径R=1，圆柱的表面积为8π；点C在底面圆O上，且∠AOC=120°．
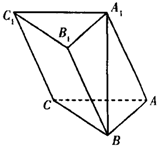如图，在三棱柱ABC-A1B1C1中，A1B⊥平面ABC，AB⊥AC．