题目内容
5.若a=log23,b=log45,$c={2^{\frac{3}{2}}}$,则a,b,c满足( )| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | c<b<a |
分析 由于2>a=log23=log49>b=log45>1,$c={2^{\frac{3}{2}}}$=$\sqrt{8}$>2,即可得出.
解答 解:∵2>a=log23=log49>b=log45>1,$c={2^{\frac{3}{2}}}$=$\sqrt{8}$>2,
∴c>a>b.
故选:B.
点评 本题考查了指数函数与对数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.设f(x)=$\left\{\begin{array}{l}{{4}^{lo{g}_{2}(x-8)}(x≥9)}\\{f[f(x+6)](x<9)}\end{array}\right.$,则f(5)的值为( )
| A. | 1 | B. | 5 | C. | 9 | D. | 11 |
16.用反证法证明结论:“曲线y=f(x)与曲线y=g(x)至少有两个不同的交点”时,要做的假设是( )
| A. | 曲线y=f(x)与曲线y=g(x)至多有两个不同的交点 | |
| B. | 曲线y=f(x)与曲线y=g(x)至多有一个交点 | |
| C. | 曲线y=f(x)与曲线y=g(x)恰有两个不同的交点 | |
| D. | 曲线y=f(x)与曲线y=g(x)至少有一个交点 |
14.某同学寒假期间对其30位亲属的饮食习惯进行了一次调查,列出了如下2×2列联表:
则可以说其亲属的饮食习惯与年龄有关的把握为( )
附:参考公式和临界值表${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d)
| 偏爱蔬菜 | 偏爱肉类 | 合计 | |
| 50岁以下 | 4 | 8 | 12 |
| 50岁以上 | 16 | 2 | 18 |
| 合计 | 20 | 10 | 30 |
附:参考公式和临界值表${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d)
| k | 2.706 | 3.841 | 6.636 | 10.828 |
| P(K2>k) | 0.10 | 0.05 | 0.010 | 0.001 |
| A. | 90% | B. | 95% | C. | 99% | D. | 99.9% |
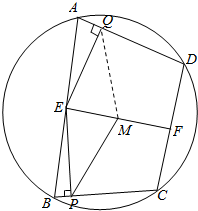 已知E、F是圆内接四边形ABCD对边AB、CD的中点,M是EF的中点,自E分别作BC、AD的垂线,垂足记为P、Q.求证:MP=MQ.
已知E、F是圆内接四边形ABCD对边AB、CD的中点,M是EF的中点,自E分别作BC、AD的垂线,垂足记为P、Q.求证:MP=MQ.