题目内容
15.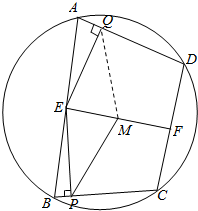 已知E、F是圆内接四边形ABCD对边AB、CD的中点,M是EF的中点,自E分别作BC、AD的垂线,垂足记为P、Q.求证:MP=MQ.
已知E、F是圆内接四边形ABCD对边AB、CD的中点,M是EF的中点,自E分别作BC、AD的垂线,垂足记为P、Q.求证:MP=MQ.
分析 过F、T作BC、AD的垂线,垂直足为X、Y、P、Q,则TX和TY为MP和NQ的垂直平分线,推导出M、N、Q、P四点共圆,得到T是圆MNQP的圆心,由此能证明TM=TN.
解答 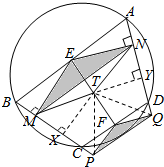 证明:如图,过F、T作BC、AD的垂线,垂直足为X、Y、P、Q,
证明:如图,过F、T作BC、AD的垂线,垂直足为X、Y、P、Q,
如图连结辅助线,则TX和TY为MP和NQ的垂直平分线,
由四点共圆知:
EN=$\frac{1}{2}AB•sinA$,EM=$\frac{1}{2}AB•sinB$,FQ=$\frac{1}{2}CD•sinB$,FQ=$\frac{1}{2}CD•sinB$,FP=$\frac{1}{2}CD•sinA$,
∴$\frac{EN}{EM}=\frac{FP}{FQ}$,又由EN∥FQ,EM∥FP,∴∠NEM=∠PFQ,
∴△NEM∽△PFQ,∴∠ENM=∠FPQ,
∴∠MNQ+∠QPM=∠MNQ+∠ENM+∠FPM=90°+90°=180°,
∴M、N、Q、P四点共圆,
∴T是圆MNQP的圆心,
∴TM=TN.
点评 本题考查线段相等的证明,是中档题,解题时要认真审题,注意四点共圆的性质的合理运用.

练习册系列答案
相关题目
5.若a=log23,b=log45,$c={2^{\frac{3}{2}}}$,则a,b,c满足( )
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | c<b<a |
3.某单位为了了解用电量y度与气温x℃之间的关系,统计了某4天的用电量与当天气温,数据如表
由表中数据可得线性回归方程$\hat y=bx+a$中的b=-2,预测当气温为5℃时,该单位用电量的度数约为50度.
| 气温(℃) | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | 38 | 64 |
10.已知复数Z=$\frac{1-i}{1+i}+{i^{2016}}$(i为虚数单位),则z的虚部是( )
| A. | 1 | B. | -1 | C. | 0 | D. | -i |
7.已知f(x)在(-∞,+∞)上是增函数,若f(4)=0,则满足x•f(x)≤0的x取值范围是( )
| A. | [0,4] | B. | (-∞,4] | C. | [-4,0)∪(0,4] | D. | [4,+∞) |