题目内容
某几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||
B、
| ||
| C、8 | ||
| D、4 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由三视图可判断几何体是三棱锥，底面直角边为2的等腰直角三角形，三棱锥的顶点在底面上的射影是底面三角形斜边的中点，代入公式可求体积．
解答：
解：由三视图知几何体为三棱锥，底面直角边为2的等腰直角三角形，
由正视图与侧视图知：三棱锥的顶点在底面上的射影是底面等腰直角三角形斜边的中点，
三棱锥的高为：
=2，
∴V=
×
×2×2×2=
．
故选：B．
由正视图与侧视图知：三棱锥的顶点在底面上的射影是底面等腰直角三角形斜边的中点，
三棱锥的高为：
(
|
∴V=
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
故选：B．
点评：本题考查由三视图求几何体的体积问题，解题的关键是由三视图判断几何体的相关元素的数据．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
在用反证法证明“自然数a，b，c中恰有一个偶数”时的正确反设应为（ ）
| A、a，b，c都是奇数 |
| B、a，b，c都是奇数或至少有两个偶数 |
| C、a，b，c都是偶数 |
| D、a，b，c中至少有两个偶数 |
已知a，b∈R，则下列命题正确的是（ ）
| A、若a＞b，则a2＞b2 |
| B、若|a|＞b，则a2＞b2 |
| C、若a＞|b|，则a2＞b2 |
| D、若a≠|b|，则a2≠b2 |
sin5°sin25°-sin95°sin65°的值是（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
甲、乙2人独立解答某道题，解答正确的概率分别为p1和p2，则甲、乙至少有1人解答正确的概率是（ ）
| A、p1+p2 |
| B、1-（1-p1）（1-p2） |
| C、1-p1p2 |
| D、p1p2 |
经过点M（2，2）且在两轴上截距相等的直线是（ ）
| A、x+y=4 |
| B、x+y=2 |
| C、x=2或y=2 |
| D、x+y=4或x=y |
一个几何体的三视图如图所示，则该几何体的体积是（ ）| A、π | B、2π | C、3π | D、4π |
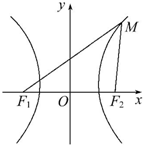如图，设有双曲线