题目内容
 已知函数f(x)=|x2-2x|-a.
已知函数f(x)=|x2-2x|-a.(1)当a=0时,画出函数f(x)的简图,并指出f(x)的单调递减区间;
(2)若函数f(x)有4个零点,求a的取值范围.
考点:函数图象的作法,根的存在性及根的个数判断
专题:函数的性质及应用
分析:(1)当a=0时,函数f(x)=|x(x-2)|的图象如图所示,由函数的图象可得f(x)的增区间和减区间.
(2)由题意可得函数f(x)的图象有4个零点,即函数y=|x2-2x|的图象和直线y=a有4个交点,结合(1)中函数的图象可得a的范围.
(2)由题意可得函数f(x)的图象有4个零点,即函数y=|x2-2x|的图象和直线y=a有4个交点,结合(1)中函数的图象可得a的范围.
解答:
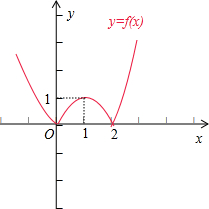 解:(1)当a=0时,函数f(x)=|x2-2x|=|x(x-2)|的图象如图所示:
解:(1)当a=0时,函数f(x)=|x2-2x|=|x(x-2)|的图象如图所示:
由函数的图象可得f(x)的增区间为[0,1]、[2,+∞);
减区间为(-∞,0)、(1,2).
(2)若函数f(x)有4个零点,则函数f(x)的图象有4个零点,
即函数y=|x2-2x|的图象和直线y=a有4个交点,
结合(1)中函数的图象可得0<a<1.
 解:(1)当a=0时,函数f(x)=|x2-2x|=|x(x-2)|的图象如图所示:
解:(1)当a=0时,函数f(x)=|x2-2x|=|x(x-2)|的图象如图所示:由函数的图象可得f(x)的增区间为[0,1]、[2,+∞);
减区间为(-∞,0)、(1,2).
(2)若函数f(x)有4个零点,则函数f(x)的图象有4个零点,
即函数y=|x2-2x|的图象和直线y=a有4个交点,
结合(1)中函数的图象可得0<a<1.
点评:本题主要考查作函数的图象,方程根的存在性以及个数判断,体现了转化、数形结合的数学思想,属于基础题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
已知
=(2,-1),
=(
,λ),则“向量
,
的夹角为锐角”是“λ<1”的( )
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |