题目内容
19.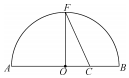 《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( )
《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( )| A. | $\frac{a+b}{2}≥\sqrt{ab}$(a>0,b>0) | B. | a2+b2≥2ab(a>0,b>0) | ||
| C. | $\frac{2ab}{a+b}≤\sqrt{ab}$(a>0,b>0) | D. | $\frac{a+b}{2}≤\sqrt{\frac{{{a^2}+{b^2}}}{2}}$(a>0,b>0) |
分析 由图形可知:OF=$\frac{1}{2}AB$=$\frac{a+b}{2}$,OC=$\frac{a-b}{2}$.在Rt△OCF中,由勾股定理可得:CF=$\sqrt{(\frac{a+b}{2})^{2}+(\frac{a-b}{2})^{2}}$=$\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$.利用CF≥OC即可得出.
解答 解:由图形可知:OF=$\frac{1}{2}AB$=$\frac{a+b}{2}$,OC=$\frac{a-b}{2}$.
在Rt△OCF中,由勾股定理可得:
CF=$\sqrt{(\frac{a+b}{2})^{2}+(\frac{a-b}{2})^{2}}$=$\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$.
∵CF≥OC,
∴$\frac{a+b}{2}$≤$\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$.(a,b>0).
故选:D.
点评 本题考查了圆的性质、勾股定理、三角形三边大小关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
15.红星超市为了了解顾客一次购买某牛奶制品的数量(单位:盒)及结算的时间(单位:分钟)等信息,随机收集了在该超市购买牛奶制品的50位顾客的相关数据,如表所示:
(Ⅰ)请估计这50位顾客购买牛奶制品的结算时间的平均值;并求一位顾客的结算时间小于结算时间平均值的概率;
(Ⅱ)从购买牛奶制品的数量不少于10盒的顾客中任选两人,求两位顾客的结算时间之和超过3.5分钟的概率.
| 一次购物数量 | 1至2盒 | 3至5盒 | 6至9盒 | 10至17盒 | 18至25盒 |
| 顾客数量(人) | 20 | 14 | 10 | 2 | 4 |
| 结算的时间(分钟/人) | 1 | 1.5 | 2 | 1.5 | 2 |
(Ⅱ)从购买牛奶制品的数量不少于10盒的顾客中任选两人,求两位顾客的结算时间之和超过3.5分钟的概率.
4.在等比数列{an}中,a3a7=4a4=4,则a8等于( )
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
8.4个不同的小球全部随意放入3个不同的盒子里,使每个盒子都不空的放法种数为( )
| A. | C${\;}_{4}^{1}$C${\;}_{4}^{3}$C${\;}_{2}^{2}$ | B. | A${\;}_{3}^{1}$A${\;}_{4}^{3}$ | ||
| C. | C${\;}_{4}^{3}$A${\;}_{2}^{2}$ | D. | ${C}_{4}^{2}{A}_{3}^{3}$ |
9.函数f(x)是定义在R上的偶函数,且 f(2)=0,当x>0时,有xf′(x)-f(x)>0恒成立,则不等式f(x)<0的解集为( )
| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0)∪(0,2) | D. | (-2,0)∪(2,+∞) |
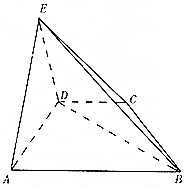 如图,在四棱锥E-ABCD中,△ADE是正三角形,侧面ADE⊥底面ABCD,AB∥DC,BD=2DC=4,AD=3,AB=5.
如图,在四棱锥E-ABCD中,△ADE是正三角形,侧面ADE⊥底面ABCD,AB∥DC,BD=2DC=4,AD=3,AB=5.