题目内容
14.已知函数f(x)=(2x2-4ax)lnx+x2.(1)设a>0,求函数f(x)的单调区间.
(2)不等式(2x-4a)lnx>-x对?x∈[1,+∞)恒成立,求a的取值范围.
分析 (1)f′(x)=(4x-4a)(lnx+1),(a>0),令f′(x)=0,得x=a,或x=$\frac{1}{e}$.分以下三种情况:①当a=$\frac{1}{e}$时,②当0$<a<\frac{1}{e}$时,③当a$>\frac{1}{e}$时,求函数的单调区间;
(2)不等式(2x-4a)lnx>-x对?x∈[1,+∞)恒成立?不等式x(2x-4a)lnx>-x2对?x∈[1,+∞)恒成立
?f(x)>0对?x∈[1,+∞)恒成立,结合(1)求解.
解答 解:(1)函数函数f(x)=(2x2-4ax)lnx+x2的定义域为(0,+∞).
f′(x)=(4x-4a)(lnx+1),(a>0),令f′(x)=0,得x=a,或x=$\frac{1}{e}$.
①当a=$\frac{1}{e}$时,f′(x)≥0在(0,+∞)恒成立,此时函数的增区间为(0,+∞),无减区间;
②当0$<a<\frac{1}{e}$时,x∈(0,a),($\frac{1}{e},+∞$)时,f′(x)>0,x$∈(a,\frac{1}{e})$时,f′(x)<0,
此时函数的增区间为(0,a),($\frac{1}{e},+∞$),减区间为:(a,$\frac{1}{e}$);
③当a$>\frac{1}{e}$时,x$∈(0,\frac{1}{e}),(a,+∞)$时,f′(x)>0,x$∈(\frac{1}{e},a)$时,f′(x)<0,
此时函数的增区间为,(0,$\frac{1}{e}$),(a,+∞),减区间为:($\frac{1}{e},a$).
(2)不等式(2x-4a)lnx>-x对?x∈[1,+∞)恒成立
?不等式x(2x-4a)lnx>-x2对?x∈[1,+∞)恒成立,
?f(x)>0对?x∈[1,+∞)恒成立,而f(1)=1>0,
由(1)得:当0<a≤1时,函数在[1,+∞)递增,f(x)≥f(1)>0,符合题意.
当a>1时,函数在(1,a)递减,在(a,+∞)递增,
故只需f(a)=a2(1-2lna)>0,即2lna<1,解得a$<\sqrt{e}$.
故1$<a<\sqrt{e}$符合题意
综上:a的取值范围为(0,$\sqrt{e}$).
点评 本题考查了利用导数求单调区间、函数最值,考查了转化思想、分类讨论思想,属于中档题.

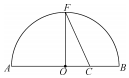 《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( )
《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( )| A. | $\frac{a+b}{2}≥\sqrt{ab}$(a>0,b>0) | B. | a2+b2≥2ab(a>0,b>0) | ||
| C. | $\frac{2ab}{a+b}≤\sqrt{ab}$(a>0,b>0) | D. | $\frac{a+b}{2}≤\sqrt{\frac{{{a^2}+{b^2}}}{2}}$(a>0,b>0) |
| A. | 2$\sqrt{2}$+1 | B. | 2$\sqrt{2}$-1 | C. | $\sqrt{6}$+1 | D. | $\sqrt{6}$-1 |
参考数据公式:$\sum_{i=1}^{6}$xiyi=1024.6,$\sum_{i=1}^{6}$xi2=730,$\overline{x}$=9,$\overline{y}$=$\frac{379}{30}$
线性回归方程:$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$
| 岁数x | 1 | 2 | 6 | 12 | 16 | 17 |
| 花费累积y(万元) | 1 | 2.8 | 9 | 17 | 22 | 24 |
(1)花费累积y与岁数x的线性回归直线方程(系数保留3位小数);
(2)24岁大学毕业之后,我们不再花父母的钱,假设你在30岁成家立业之后,在你50岁之前偿还父母为你的花费(不计利总),那么你每月要偿还父母约多少元钱?