题目内容
15.红星超市为了了解顾客一次购买某牛奶制品的数量(单位:盒)及结算的时间(单位:分钟)等信息,随机收集了在该超市购买牛奶制品的50位顾客的相关数据,如表所示:| 一次购物数量 | 1至2盒 | 3至5盒 | 6至9盒 | 10至17盒 | 18至25盒 |
| 顾客数量(人) | 20 | 14 | 10 | 2 | 4 |
| 结算的时间(分钟/人) | 1 | 1.5 | 2 | 1.5 | 2 |
(Ⅱ)从购买牛奶制品的数量不少于10盒的顾客中任选两人,求两位顾客的结算时间之和超过3.5分钟的概率.
分析 (Ⅰ)求出平均数,得到小于结算时间的平均值的人数,从而求出满足条件的概率即可;
(Ⅱ)得到买10至17盒有2人,设为a1,a2,买18至25盒有4人,设为b1,b2,b3,b4,求出满足条件的概率即可.
解答 解:(Ⅰ)由已知得$\frac{1×20+14×1.5+2×10+2×1.5+4×2}{50}$=$\frac{72}{50}$=1.44…(2分)
则小于结算时间的平均值的人数共20人,
所以一位顾客的结算时间小于结算时间的平均值的概率为p=$\frac{20}{50}$=$\frac{2}{5}$…(5分)
(Ⅱ)购买牛奶制品的数量不少于10盒的顾客共有6人,
其中买10至17盒有2人,设为a1,a2,买18至25盒有4人,设为b1,b2,b3,b4.
任选两人的情况有共15种…(9分)
其中两位顾客的结算时间之和超过3.5分钟的情况有:
{b1,b2},{b1,b3},{b1,b4},{b2,b3},{b2,b4},{b3,b4}共6种…(10分)
所以两位顾客的结算时间之和超过3.5分钟的概率$P=\frac{6}{15}=\frac{2}{5}$…(12分)
点评 本题考查学生的阅读能力,考查概率的计算,考查互斥事件,将事件分拆成互斥事件的和是解题的关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.在△ABC中,BC=5,AC=8,C=60°,则$\overrightarrow{BC}•\overrightarrow{CA}$=( )
| A. | 20 | B. | -20 | C. | $20\sqrt{3}$ | D. | $-20\sqrt{3}$ |
19.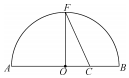 《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( )
《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( )
 《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( )
《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( )| A. | $\frac{a+b}{2}≥\sqrt{ab}$(a>0,b>0) | B. | a2+b2≥2ab(a>0,b>0) | ||
| C. | $\frac{2ab}{a+b}≤\sqrt{ab}$(a>0,b>0) | D. | $\frac{a+b}{2}≤\sqrt{\frac{{{a^2}+{b^2}}}{2}}$(a>0,b>0) |
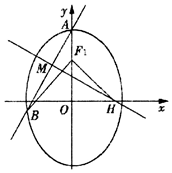 已知椭圆C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的上、下焦点分别为F1,F2,上焦点F1到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=$\frac{1}{2}$.
已知椭圆C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的上、下焦点分别为F1,F2,上焦点F1到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=$\frac{1}{2}$.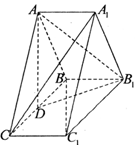 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,D为棱BC的中点,AB=AC,BC=$\sqrt{2}A{A_1}$,求证:
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,D为棱BC的中点,AB=AC,BC=$\sqrt{2}A{A_1}$,求证: