题目内容
20．在空间中，下列命题正确的是（ ）| A． | 若平面α内有无数条直线与直线l平行，则l∥α | |
| B． | 若平面α内有无数条直线与平面β平行，则α∥β | |
| C． | 若平面α内有无数条直线与直线l垂直，则l⊥α | |
| D． | 若平面α内有无数条直线与平面β垂直，则α⊥β |
分析 A，根据线面平行的判定判断；
B，根据面面平行的判定判定；
C，若平面α内有无数条直线与直线l垂直，则l与α可能斜交；
D，若平面α内有无数条直线与平面β垂直，则平面α经过平面β的垂线，则α⊥β．
解答 解：对于A，若平面α内有无数条直线与直线l平行，则l与α可能相交，故错；
对于B，若平面α内有无数条直线与平面β平行，则α与β可能相交，故错；
对于C，若平面α内有无数条直线与直线l垂直，则l与α可能斜交，故错；
对于D，若平面α内有无数条直线与平面β垂直，则平面α经过平面β的垂线，则α⊥β，故正确．
故选：D
点评 本题考查了命题真假的判定，考查了空间线面、面面位置关系，属于中档题．
练习册系列答案
相关题目
11．
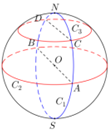如图，N、S是球O直径的两个端点，圆C1是经过N和S点的大圆，圆C2和圆C3分别是所在平面与NS垂直的大圆和小圆，圆C1和C2交于点A、B，圆C1和C3交于点C、D，设a、b、c分别表示圆C1上劣弧CND的弧长、圆C2上半圆弧AB的弧长、圆C3上半圆弧CD的弧长，则a、b、c的大小关系为（ ）
如图，N、S是球O直径的两个端点，圆C1是经过N和S点的大圆，圆C2和圆C3分别是所在平面与NS垂直的大圆和小圆，圆C1和C2交于点A、B，圆C1和C3交于点C、D，设a、b、c分别表示圆C1上劣弧CND的弧长、圆C2上半圆弧AB的弧长、圆C3上半圆弧CD的弧长，则a、b、c的大小关系为（ ）| A． | b＞a=c | B． | b=c＞a | C． | b＞a＞c | D． | b＞c＞a |
15．已知全集U={1，2，3，4}，若A={1，3}，则∁UA=（ ）
| A． | {1，2} | B． | {1，4} | C． | {2，3} | D． | {2，4} |
5．过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左顶点A作倾斜角为45°的直线l，l交y轴于点B，交双曲线的一条渐近线于点C，若$\overrightarrow{AB}$=$\overrightarrow{BC}$，则该双曲线的离心率为（ ）
| A． | 5 | B． | $\sqrt{5}$ | C． | $\sqrt{3}$ | D． | $\frac{\sqrt{5}}{2}$ |
如图是正方体平面展开图，在这个正方体中：