题目内容
19.已知函数f(x)=sin2ωx+2$\sqrt{3}$cosωxsinωx+sin(ωx+$\frac{π}{4}$)sin(ωx-$\frac{π}{4}$)(ω>0),且f(x)的最小正周期为π.(1)求ω的值;
(2)求函数f(x)在区间(0,π)上的单调增区间.
分析 (1)利用辅助角公式及二倍角公式求得f(x),由函数的周期公式,即可求得ω的值;
(2)由(1)可知,利用函数的单调性,求得$kπ-\frac{π}{6}≤x≤kπ+\frac{π}{3},k∈Z$,即可求得f(x)在区间(0,π)上的单调增区间.
解答 解:(1)f(x)=sin2ωx+2$\sqrt{3}$cosωxsinωx+sin(ωx+$\frac{π}{4}$)sin(ωx-$\frac{π}{4}$),
=$\frac{1-cos2x}{2}$+$\sqrt{3}$sin2ωx-$\frac{1}{2}$(cos2ωx-sin2ωx),
=$2sin({2ωx-\frac{π}{6}})+\frac{1}{2}$;…(5分)
由题意得$\frac{2π}{2ω}=π$,即可得ω=1…(6分)
(2)由(1)知$f(x)=2sin({2x-\frac{π}{6}})+\frac{1}{2}$
则由函数单调递增性可知:$2kπ-\frac{π}{2}≤2x-\frac{π}{6}≤2kπ+\frac{π}{2},k∈Z$
整理得:$kπ-\frac{π}{6}≤x≤kπ+\frac{π}{3},k∈Z$…(9分)
∴f(x)在(0,π)上的增区间为$({0,\frac{π}{3}}]$,$[{\frac{5π}{6},π})$…(12分)
点评 本题考查正弦函数的性质,考查辅助角公式及二倍角公式的应用,考查计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.复数z=(a+i)(-3+ai)(a∈R),若z<0,则a的值是( )
| A. | a=$\sqrt{3}$ | B. | a=-$\sqrt{3}$ | C. | a=-1 | D. | a=1 |
14.已知f(x)是定义在R上的偶函数,且在区间(-∞,0)上单调递减,若实数a满足f(3|2a+1|)>f(-$\sqrt{3}$),则a的取值范围是( )
| A. | (-∞,-$\frac{3}{4}$)∪(-$\frac{1}{4}$,+∞) | B. | (-∞,-$\frac{3}{4}$) | C. | (-$\frac{1}{4}$,+∞) | D. | (-$\frac{3}{4}$,-$\frac{1}{4}$) |
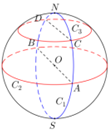 如图,N、S是球O直径的两个端点,圆C1是经过N和S点的大圆,圆C2和圆C3分别是所在平面与NS垂直的大圆和小圆,圆C1和C2交于点A、B,圆C1和C3交于点C、D,设a、b、c分别表示圆C1上劣弧CND的弧长、圆C2上半圆弧AB的弧长、圆C3上半圆弧CD的弧长,则a、b、c的大小关系为( )
如图,N、S是球O直径的两个端点,圆C1是经过N和S点的大圆,圆C2和圆C3分别是所在平面与NS垂直的大圆和小圆,圆C1和C2交于点A、B,圆C1和C3交于点C、D,设a、b、c分别表示圆C1上劣弧CND的弧长、圆C2上半圆弧AB的弧长、圆C3上半圆弧CD的弧长,则a、b、c的大小关系为( )