题目内容
19.下列命题错误的是( )| A. | 命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0则x2+y2≠0”. | |
| B. | 若命题$p:?{x_0}∈R,x_0^2-{x_0}+1≤0$,则?p:?x∈R,x2-x+1>0. | |
| C. | △ABC中,sinA>sinB是A>B的充要条件. | |
| D. | ?φ∈R,函数f(x)=sin(2x+φ)都不是偶函数. |
分析 A.根据逆否命题的定义进行判断.
B.根据含有量词的命题的否定进行判断.
C.根据正弦定理以及充分条件和必要条件的定义进行判断.
D.根据三角函数的性质结合全称命题的定义进行判断.
解答 解:A.命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0则x2+y2≠0”.正确,
B.命题是特称命题,则命题的否定为:?x∈R,x2-x+1>0,正确.
C.在三角形中,若sinA>sinB,则由正弦定理得a>b,则A>B,反之也成立,
即△ABC中,sinA>sinB是A>B的充要条件,正确.
D.当φ=$\frac{π}{2}$时,f(x)=sin(2x+$\frac{π}{2}$)=cos2x,此时函数f(x)为偶函数,故D错误,
故选:D
点评 本题主要考查命题的真假判断,涉及四种命题的关系,充分条件和必要条件的判断,以及含有量词的命题的否定,涉及的知识点较多.

练习册系列答案
相关题目
10.已知函数f(x)=x2+2bx的图象在点A(0,f(0))处的切线l与直线x+y+3=0垂直,若数列{$\frac{1}{f(n)}$}的前n项和为Sn,则S2011的值为( )
| A. | $\frac{2012}{2011}$ | B. | $\frac{2010}{2011}$ | C. | $\frac{2013}{2012}$ | D. | $\frac{2011}{2012}$ |
4.已知{an}是首项为1的等比数列,且a4=8,则数列$\left\{{\frac{1}{a_n}}\right\}$的前5项和为( )
| A. | 31 | B. | $\frac{31}{16}$ | C. | 11 | D. | $\frac{11}{16}$ |
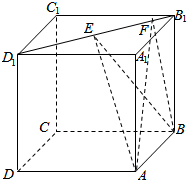 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{1}{2}$,则下列结论中正确的序号是①②③.
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{1}{2}$,则下列结论中正确的序号是①②③.