题目内容
4.已知{an}是首项为1的等比数列,且a4=8,则数列$\left\{{\frac{1}{a_n}}\right\}$的前5项和为( )| A. | 31 | B. | $\frac{31}{16}$ | C. | 11 | D. | $\frac{11}{16}$ |
分析 求出数列的公比,锐角利用等比数列求和公式求解即可.
解答 解:{an}是首项为1的等比数列,且a4=8,可得q3=8,可得q=2,
数列$\left\{{\frac{1}{a_n}}\right\}$也是等比数列,公比为:$\frac{1}{2}$,首项为1.
它的前5项和为:$\frac{1-{(\frac{1}{2})}^{5}}{1-\frac{1}{2}}$=$\frac{31}{16}$.
故选:B.
点评 本题考查等比数列求和公式的应用,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列命题错误的是( )
| A. | 命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0则x2+y2≠0”. | |
| B. | 若命题$p:?{x_0}∈R,x_0^2-{x_0}+1≤0$,则?p:?x∈R,x2-x+1>0. | |
| C. | △ABC中,sinA>sinB是A>B的充要条件. | |
| D. | ?φ∈R,函数f(x)=sin(2x+φ)都不是偶函数. |
16.某几何体的三视图如图所示,则该几何体外接球的表面积为( )
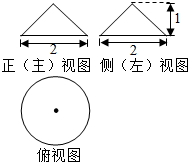

| A. | 4π | B. | π | C. | $\frac{π}{2}$ | D. | 2π |
13.若动点P(x,y)在$\frac{x^2}{4}+\frac{y^2}{9}=1$曲线上变化,则x2+2y的最大值为( )
| A. | $\frac{25}{4}$ | B. | $\frac{27}{4}$ | C. | 6 | D. | 8 |
14.如果椭圆$\frac{x^2}{81}+\frac{y^2}{25}=1$上一点M到此椭圆一个焦点F1的距离为10,N是MF1的中点,O是坐标原点,则ON的长为( )
| A. | 2 | B. | 4 | C. | 8 | D. | $\frac{3}{2}$ |
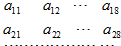 (理)64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行都成等差数列,而每一列都成等比数列(且每列公比都相等).若a11=$\frac{1}{2}$,a24=1,a32=$\frac{1}{4}$.则a81a82…a88…aij=j($\frac{1}{2}$)i.
(理)64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行都成等差数列,而每一列都成等比数列(且每列公比都相等).若a11=$\frac{1}{2}$,a24=1,a32=$\frac{1}{4}$.则a81a82…a88…aij=j($\frac{1}{2}$)i.