题目内容
9.函数f(x)=x2-ax+a(x∈R),数列$\{a_n^{\;}\}$的前n项和Sn=f(n),且f(x)同时满足:①不等式f(x)≤0的解集有且只有一个元素;②在定义域内存在0<x1<x2,使得不等式f(x1)>f(x2)成立.(1)求函数f(x)的表达式;
(2)求数列$\{a_n^{\;}\}$的通项公式.
分析 (1)由①可得判别式为0,解得a=0或4,讨论a=0和4,结合条件②,可得f(x)的解析式;
(2)求得Sn=(n-2)2,由n=1时,a1=S1,n>1时,an=Sn-Sn-1,即可得到所求数列的通项.
解答 解:(1)不等式f(x)≤0的解集有且只有一个元素,
可得△=a2-4a=0,则a=0或a=4,
当a=0,f(x)=x2在(0,+∞)上是单调递增的,不符合题目要求舍去;
当a=4,f(x)=x2-4x+4在(0,2)上是单调递减(2,+∞)单调增的,符合题意.
所以a=4,f(x)=x2-4x+4;
(2)${S_n}=f(n)={n^2}-4n+4={(n-2)^2}$,
n=1时,a1=S1=1,
$n≥2时,{a_n}={S_n}-{S_{n-1}}={(n-2)^2}-{(n-3)^2}=2n-5$.
所以${a_n}=\left\{{\begin{array}{l}{1,n=1}\\{2n-5,n≥2}\end{array}}\right.$.
点评 本题考查二次不等式的解法和函数的单调性的运用,考查数列的通项公式的求法,注意n=1时的情况,属于基础题和易错题.

练习册系列答案
相关题目
17.已知$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(1,λ),且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ为锐角,则实数λ的取值范围是( )
| A. | (-∞,-2)∪(-2,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,+∞) | C. | (-2,$\frac{2}{3}$)∪($\frac{2}{3}$,+∞) | D. | (-∞,$\frac{1}{2}$) |
1.函数$y=2sin(\frac{π}{3}-x)-cos(\frac{π}{6}+x)(0≤x≤π)$的值域是( )
| A. | $[-1,\frac{{\sqrt{3}}}{2}]$ | B. | [-1,1] | C. | $[-\frac{{\sqrt{3}}}{2},\frac{{\sqrt{3}}}{2}]$ | D. | $[-\frac{{\sqrt{3}}}{2},1]$ |
19.下列命题错误的是( )
| A. | 命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0则x2+y2≠0”. | |
| B. | 若命题$p:?{x_0}∈R,x_0^2-{x_0}+1≤0$,则?p:?x∈R,x2-x+1>0. | |
| C. | △ABC中,sinA>sinB是A>B的充要条件. | |
| D. | ?φ∈R,函数f(x)=sin(2x+φ)都不是偶函数. |
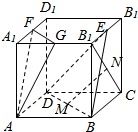 如图,在正方体ABCD-A1B1C1D1中,E,F,G,M,N分别是B1C1,A1D1,A1B1,BD,B1C的中点,求证:
如图,在正方体ABCD-A1B1C1D1中,E,F,G,M,N分别是B1C1,A1D1,A1B1,BD,B1C的中点,求证: