题目内容
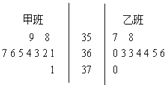 为检测学生的体温状况,随机抽取甲,乙两个班级各10名同学,测量他们的体温(单位0.1摄氏度)获得体温数据的茎叶图,如图所示.
为检测学生的体温状况,随机抽取甲,乙两个班级各10名同学,测量他们的体温(单位0.1摄氏度)获得体温数据的茎叶图,如图所示.(Ⅰ)根据茎叶图判断哪个班级的平均体温较高;
(Ⅱ)计算乙班的样本方差.
考点:极差、方差与标准差
专题:概率与统计
分析:(Ⅰ)根据茎叶图,求出甲、乙的平均数,比较即可得出结论;
(Ⅱ)根据方差计算公式求出乙班的样本方差即可.
(Ⅱ)根据方差计算公式求出乙班的样本方差即可.
解答:
解:(Ⅰ)根据茎叶图,得;
甲的平均数为
=
(35.8+35.9+36.1+36.2+36.3+36.4+36.5+36.6+36.7+37.1)=36.36,
乙的平均数为
=
(35.7+35.8+36.0+36.3+36.3+36.4+36.4+36.5+36.6+37.0)=36.3,
∴甲班学生的平均体温较高些;
(Ⅱ)乙班的样本方差为
s乙2=
[(35.7-36.3)2+(35.8-36.3)2+(36.0-36.3)2+(36.3-36.3)2+(36.3-36.3)2
+(36.4-36.3)2+(36.4-36.3)2+(36.5-36.3)2+(36.6-36.3)2+(37.0-36.3)2]=13.4.
甲的平均数为
. |
| x甲 |
| 1 |
| 10 |
乙的平均数为
. |
| x乙 |
| 1 |
| 10 |
∴甲班学生的平均体温较高些;
(Ⅱ)乙班的样本方差为
s乙2=
| 1 |
| 10 |
+(36.4-36.3)2+(36.4-36.3)2+(36.5-36.3)2+(36.6-36.3)2+(37.0-36.3)2]=13.4.
点评:本题考查了利用茎叶图中的数据求平均数与方差的问题,是基础题目.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
已知曲线
+
=1(m<6)与曲线
+
=1(5<m<9),则两曲线的( )
| x2 |
| 10-m |
| y2 |
| 6-m |
| x2 |
| 5-m |
| y2 |
| 9-m |
| A、顶点相同 | B、焦点相同 |
| C、焦距相等 | D、离心率相等 |
设条件p:
≥0条件(x-1)(x+2)≥0.则p是q的( )
| x-1 |
| x+2 |
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
 如图,已知椭圆C:
如图,已知椭圆C: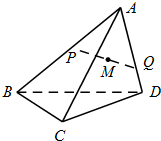 如图,在三棱锥A-BCD中,三条侧棱AB,AC,AD两两垂直,AB=AC=AD=6,P,Q分别是侧面ABC和棱AD上动点,PQ=4,M为线段PQ中点,当P,Q运动时,点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比等于
如图,在三棱锥A-BCD中,三条侧棱AB,AC,AD两两垂直,AB=AC=AD=6,P,Q分别是侧面ABC和棱AD上动点,PQ=4,M为线段PQ中点,当P,Q运动时,点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比等于