题目内容
已知曲线
+
=1(m<6)与曲线
+
=1(5<m<9),则两曲线的( )
| x2 |
| 10-m |
| y2 |
| 6-m |
| x2 |
| 5-m |
| y2 |
| 9-m |
| A、顶点相同 | B、焦点相同 |
| C、焦距相等 | D、离心率相等 |
考点:双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由m的范围分别得到两种曲线的类型,由隐含条件求得两曲线的焦距得答案.
解答:
解:∵m<6,∴曲线
+
=1表示焦点在x轴上的椭圆,
则a2=10-m,b2=6-m,c2=a2-b2=10-m-6+m=4,c=2;
由5<m<9,可知曲线
+
=1表示焦点在y轴上的双曲线,
则a2=9-m,b2=-5+m,c2=a2+b2=9-m-5+m=4,c=2.
∴曲线
+
1(m<6)与曲线
+
=1(5<m<9)的焦距相等.
故选:C.
| x2 |
| 10-m |
| y2 |
| 6-m |
则a2=10-m,b2=6-m,c2=a2-b2=10-m-6+m=4,c=2;
由5<m<9,可知曲线
| x2 |
| 5-m |
| y2 |
| 9-m |
则a2=9-m,b2=-5+m,c2=a2+b2=9-m-5+m=4,c=2.
∴曲线
| x2 |
| 10-m |
| y2 |
| 6-m |
| x2 |
| 5-m |
| y2 |
| 9-m |
故选:C.
点评:本题考查了椭圆和双曲线的标准方程,考查了椭圆和双曲线的简单几何性质,是基础题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
对同一目标进行三次射击,第一、二、三次射击命中目标的概率分别为0.4,0.5和0.7,则三次射击中恰有二次命中目标的概率是( )
| A、0.41 | B、0.64 |
| C、0.74 | D、0.63 |
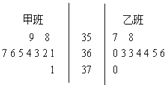 为检测学生的体温状况,随机抽取甲,乙两个班级各10名同学,测量他们的体温(单位0.1摄氏度)获得体温数据的茎叶图,如图所示.
为检测学生的体温状况,随机抽取甲,乙两个班级各10名同学,测量他们的体温(单位0.1摄氏度)获得体温数据的茎叶图,如图所示.