题目内容
PA⊥平面ABC,∠ACB=90°且PA=AC=BC=1,则异面直线PB与AC所成角的正切值为 .
考点:直线与平面垂直的性质,异面直线及其所成的角
专题:计算题,空间位置关系与距离
分析:过B作BD∥AC,且BD=AC;所以ADBC为矩形且∠PBD(或其补角)即为所求.根据已知即可求出其正切值.
解答:
 解:过B作BD∥AC,且BD=AC;
解:过B作BD∥AC,且BD=AC;
所以ADBC为矩形
且∠PBD(或其补角)即为所求.
因为PA=AC=BC=1
∴AD=1;BD=1
∵PA⊥平面ABC
∴PD=
=
;
又因为PA⊥DB,DB⊥AD∴DB⊥平面PAD∴BD⊥PD.
在RT△PDB中,tan∠PBD=
=
.
即异面直线PB与AC所成的角的正切值等于
故答案为:
 解:过B作BD∥AC,且BD=AC;
解:过B作BD∥AC,且BD=AC;所以ADBC为矩形
且∠PBD(或其补角)即为所求.
因为PA=AC=BC=1
∴AD=1;BD=1
∵PA⊥平面ABC
∴PD=
| PA2+AD2 |
| 2 |
又因为PA⊥DB,DB⊥AD∴DB⊥平面PAD∴BD⊥PD.
在RT△PDB中,tan∠PBD=
| ||
| 1 |
| 2 |
即异面直线PB与AC所成的角的正切值等于
| 2 |
故答案为:
| 2 |
点评:本题主要考察了直线与平面垂直的性质,异面直线及其所成的角,属于基本知识的考查.

练习册系列答案
相关题目
若方程y2-x2lga=
-a表示焦点在x轴上的椭圆,则a的取值范围是( )
| 1 |
| 3 |
A、(0 ,
| ||||
B、(
| ||||
C、(0 ,
| ||||
D、(
|
若一个圆锥的轴截面是等边三角形,其面积为
,则这个圆锥的体积为( )
| 3 |
| A、3π | ||||
B、
| ||||
C、
| ||||
D、
|
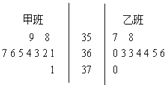 为检测学生的体温状况,随机抽取甲,乙两个班级各10名同学,测量他们的体温(单位0.1摄氏度)获得体温数据的茎叶图,如图所示.
为检测学生的体温状况,随机抽取甲,乙两个班级各10名同学,测量他们的体温(单位0.1摄氏度)获得体温数据的茎叶图,如图所示.