题目内容
过点M(1,1)斜率为-
的直线与椭圆交于A、B两点,若M为AB中点,则e= .
| 1 |
| 2 |
考点:椭圆的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:设椭圆方程为
+
=1(a>b>0),A(x1,y1),B(x2,y2),代入椭圆方程,两式相减,由于平方差公式,结合中点坐标公式和斜率公式,可得a2=2b2,再由a,b,c的关系和离心率公式,即可得到.
| x2 |
| a2 |
| y2 |
| b2 |
解答:
解:设椭圆方程为
+
=1(a>b>0),
A(x1,y1),B(x2,y2),
则有
+
=1,
+
=1,
两式相减可得,
+
=0,
由于M为AB中点,则有x1+x2=2,y1+y2=2,
则kAB=
=-
=-
,
即a2=2b2=2(a2-c2),则a=
c,
则有e=
=
.
故答案为:
.
| x2 |
| a2 |
| y2 |
| b2 |
A(x1,y1),B(x2,y2),
则有
| x12 |
| a2 |
| y12 |
| b2 |
| x22 |
| a2 |
| y22 |
| b2 |
两式相减可得,
| (x1-x2)(x1+x2) |
| a2 |
| (y1-y2)(y1+y2) |
| b2 |
由于M为AB中点,则有x1+x2=2,y1+y2=2,
则kAB=
| y1-y2 |
| x1-x2 |
| b2 |
| a2 |
| 1 |
| 2 |
即a2=2b2=2(a2-c2),则a=
| 2 |
则有e=
| c |
| a |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查椭圆的方程和性质,考查离心率的求法,考查点差法解决中点弦的问题,考查运算能力,属于中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
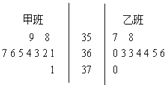 为检测学生的体温状况,随机抽取甲,乙两个班级各10名同学,测量他们的体温(单位0.1摄氏度)获得体温数据的茎叶图,如图所示.
为检测学生的体温状况,随机抽取甲,乙两个班级各10名同学,测量他们的体温(单位0.1摄氏度)获得体温数据的茎叶图,如图所示.