题目内容
 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆的标准方程;
(2)过点M作两条直线分别交椭圆于A、B两点,若两直线与x轴所围成的三角形为等边三角形:
①求证:AB∥OM;
②求△MAB面积的最大值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由于椭圆C:
+
=1(a>b>0)的离心率为
,且经过点M(2,1).可得
,解得即可.
(2))①证明:两直线与x轴所围成的三角形为等边三角形,可得直线AM,BM的方程分别为:y-1=
(x-2),y-1=-
(x-2),与椭圆方程联立化为13x2+8(
-6)x+44-16
=0,解得xA,yA.同理可得xB,yB.证明kAB=
=kOM=
,即可.②由①可设直线AB的方程为y=
x+t.与椭圆方程联立x2+2tx+2t2-8=0,由于△>0,可得根与系数的关系,|AB|=
,利用点到直线的距离公式可得点M到直线AB的距离d.再利用S△MAB=
d•|AB|,及其导数研究函数的单调性即可得出.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
|
(2))①证明:两直线与x轴所围成的三角形为等边三角形,可得直线AM,BM的方程分别为:y-1=
| 3 |
| 3 |
| 3 |
| 3 |
| yB-yA |
| xB-xA |
| 1 |
| 2 |
| 1 |
| 2 |
(1+
|
| 1 |
| 2 |
解答:
解:(1)∵椭圆C:
+
=1(a>b>0)的离心率为
,且经过点M(2,1).
∴
,解得a2=8,b2=2,
∴椭圆C的标准方程为
+
=1.
(2)①证明:两直线与x轴所围成的三角形为等边三角形,可得直线AM,BM的方程分别为:y-1=
(x-2),y-1=-
(x-2),
联立
,化为13x2+8(
-6)x+44-16
=0,
∴2×xA=
,∴xA=
.yA=
.
同理可得xB=
,yB=
.
∴kAB=
=
,
∵kOM=
,
∴kOM=kAB.
∴OA∥AB.
②由①可设直线AB的方程为y=
x+t.
联立
,化为x2+2tx+2t2-8=0,
△=4t2-4(2t2-8)>0,化为t2<8.
∴x1+x2=-2t,x1x2=2t2-8.
∴|AB|=
=
=
.
点M到直线AB的距离d=
=
.
∴S△MAB=
d•|AB|=
×
×
=
,
令g(t)=8t-t3,(t2<8).
g′(t)=8-3t2,
令g′(t)>0,解得t2<
,此时函数g(t)单调递增;令g′(t)<0,解得8>t2>
,此时函数g(t)单调递减.
∴当t2=
(满足t2<8)时,函数g(t)取得最大值,8×
-(
)3=
.
∴△MAB取得最大值为
=
.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
∴
|
∴椭圆C的标准方程为
| x2 |
| 8 |
| y2 |
| 2 |
(2)①证明:两直线与x轴所围成的三角形为等边三角形,可得直线AM,BM的方程分别为:y-1=
| 3 |
| 3 |
联立
|
| 3 |
| 3 |
∴2×xA=
44-16
| ||
| 13 |
22-8
| ||
| 13 |
-11-4
| ||
| 13 |
同理可得xB=
22+8
| ||
| 13 |
4
| ||
| 13 |
∴kAB=
| yB-yA |
| xB-xA |
| 1 |
| 2 |
∵kOM=
| 1 |
| 2 |
∴kOM=kAB.
∴OA∥AB.
②由①可设直线AB的方程为y=
| 1 |
| 2 |
联立
|
△=4t2-4(2t2-8)>0,化为t2<8.
∴x1+x2=-2t,x1x2=2t2-8.
∴|AB|=
(1+
|
|
| 40-5t2 |
点M到直线AB的距离d=
| |2-2+2t| | ||
|
| |2t| | ||
|
∴S△MAB=
| 1 |
| 2 |
| 1 |
| 2 |
| |2t| | ||
|
| 40-5t2 |
| 8t-t3 |
令g(t)=8t-t3,(t2<8).
g′(t)=8-3t2,
令g′(t)>0,解得t2<
| 8 |
| 3 |
| 8 |
| 3 |
∴当t2=
| 8 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
| 64 |
| 27 |
∴△MAB取得最大值为
|
8
| ||
| 9 |
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交转化为方程联立可得根与系数的关系、弦长公式、点到直线的距离公式、三角形的面积计算公式、利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
正三棱柱ABC-A1B1C1中,若AB=2,AA1=1,若则点A到平面A1BC的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
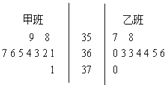 为检测学生的体温状况,随机抽取甲,乙两个班级各10名同学,测量他们的体温(单位0.1摄氏度)获得体温数据的茎叶图,如图所示.
为检测学生的体温状况,随机抽取甲,乙两个班级各10名同学,测量他们的体温(单位0.1摄氏度)获得体温数据的茎叶图,如图所示.