题目内容
已知函数f(x)=4sinxcos(x+
)+
.
(1)当tanα=2时,求f(α)的值;
(2)求f(x)在区间[-
,
]上的值域.
| π |
| 3 |
| 3 |
(1)当tanα=2时,求f(α)的值;
(2)求f(x)在区间[-
| π |
| 4 |
| π |
| 6 |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的求值,三角函数的图像与性质
分析:(1)由三角函数的公式化简可得f(x)=2sin(2x+
),由万能公式可得答案;
(2)由x的范围可得2x+
的范围,进而可得sin(2x+
)的范围,可得f(x)的范围,结合三角函数在该区间的单调性,可得最值及对应的x值.
| π |
| 3 |
(2)由x的范围可得2x+
| π |
| 3 |
| π |
| 3 |
解答:
解:(1)化简可得f(x)=4sinx(cosxcos
-sinxsin
)+
=2sinxcosx-2
sin2x+
=sin2x+
cos2x…(2分)
=2sin(2x+
)…(4分)
∵tanα=2,
∴f(α)=2sin(2α+
)=sin2α+
cos2α=
+
=
;…(7分)
(2)因为x∈[-
,
],所以-
≤2x+
≤
…(9分)
所以-
≤sin(2x+
)≤1,所以-1≤f(x)≤2,
当2x+
=-
,即x=-
时,f(x)min=-1,
当2x+
=
,即x=
时,f(x)max=2,…(14分)
| π |
| 3 |
| π |
| 3 |
| 3 |
=2sinxcosx-2
| 3 |
| 3 |
=sin2x+
| 3 |
=2sin(2x+
| π |
| 3 |
∵tanα=2,
∴f(α)=2sin(2α+
| π |
| 3 |
| 3 |
| 2tanα |
| 1+tan2α |
| ||
| 1+tan2α |
4-3
| ||
| 5 |
(2)因为x∈[-
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
所以-
| 1 |
| 2 |
| π |
| 3 |
当2x+
| π |
| 3 |
| π |
| 6 |
| π |
| 4 |
当2x+
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
点评:本题考查两角和与差的正弦函数,涉及三角函数的周期性和值域,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=3sinx-3
cosx的最大值是( )
| 3 |
A、3+3
| ||
B、4
| ||
| C、6 | ||
| D、3 |
若一个圆锥的轴截面是等边三角形,其面积为
,则这个圆锥的体积为( )
| 3 |
| A、3π | ||||
B、
| ||||
C、
| ||||
D、
|
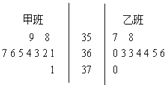 为检测学生的体温状况,随机抽取甲,乙两个班级各10名同学,测量他们的体温(单位0.1摄氏度)获得体温数据的茎叶图,如图所示.
为检测学生的体温状况,随机抽取甲,乙两个班级各10名同学,测量他们的体温(单位0.1摄氏度)获得体温数据的茎叶图,如图所示.