题目内容
已知数列{an}是等差数列,a1=-6,a3,a5,a6成等比数列且互不相等.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{an}的前n项和为Sn,k是整数,若不等式Sn>an对一切n≥k的正整数n都成立,求k的最小值.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{an}的前n项和为Sn,k是整数,若不等式Sn>an对一切n≥k的正整数n都成立,求k的最小值.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)设出等差数列的公差,由a3,a5,a6成等比数列列式求得等差数列的公差,则等差数列的通项公式可求;
(Ⅱ)求出等差数列的前n项和,由Sn>an求得n的范围,再结合不等式对一切n≥k的正整数n都成立求得k的最小值.
(Ⅱ)求出等差数列的前n项和,由Sn>an求得n的范围,再结合不等式对一切n≥k的正整数n都成立求得k的最小值.
解答:
解:(Ⅰ)设数列{an}的公差为d.
由已知得a52=a3•a6,即(-6+4d)2=(-6+2d)•(-6+5d),
解得:d=0(舍去)或d=1,
故an=-6+(n-1)•1=n-7;
(Ⅱ)Sn=
=
=
.
不等式Sn>an,等价于
>n-7.
∴n2-15n+14>0,解得n<1或n>14,n∈N.
又对一切n≥k的正整数n都成立,
∴正整数k的最小值为15.
由已知得a52=a3•a6,即(-6+4d)2=(-6+2d)•(-6+5d),
解得:d=0(舍去)或d=1,
故an=-6+(n-1)•1=n-7;
(Ⅱ)Sn=
| n(a1+an) |
| 2 |
| n(-6+n-7) |
| 2 |
| n(n-13) |
| 2 |
不等式Sn>an,等价于
| n(n-13) |
| 2 |
∴n2-15n+14>0,解得n<1或n>14,n∈N.
又对一切n≥k的正整数n都成立,
∴正整数k的最小值为15.
点评:本题考查了等差数列的性质,考查了等差数列的前n项和,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
对同一目标进行三次射击,第一、二、三次射击命中目标的概率分别为0.4,0.5和0.7,则三次射击中恰有二次命中目标的概率是( )
| A、0.41 | B、0.64 |
| C、0.74 | D、0.63 |
函数y=3sinx-3
cosx的最大值是( )
| 3 |
A、3+3
| ||
B、4
| ||
| C、6 | ||
| D、3 |
若方程y2-x2lga=
-a表示焦点在x轴上的椭圆,则a的取值范围是( )
| 1 |
| 3 |
A、(0 ,
| ||||
B、(
| ||||
C、(0 ,
| ||||
D、(
|
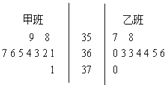 为检测学生的体温状况,随机抽取甲,乙两个班级各10名同学,测量他们的体温(单位0.1摄氏度)获得体温数据的茎叶图,如图所示.
为检测学生的体温状况,随机抽取甲,乙两个班级各10名同学,测量他们的体温(单位0.1摄氏度)获得体温数据的茎叶图,如图所示.