题目内容
双曲线的渐近线方程为2x±y=0,两顶点间的距离为4,则双曲线的方程为 .
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先确定a的值,再分类讨论,求出b的值,即可得到双曲线的标准方程.
解答:
解:由题意2a=4,∴a=2,
当焦点在x轴上时,∵双曲线的渐近线方程为y=±2x,∴
=2,∴b=4,
∴方程为
-
=1;
当焦点在y轴上时,∵双曲线的渐近线方程为y=±2x,∴
=2,∴b=1,
∴方程为
-x2=1.
故答案为:
-
=1或
-x2=1.
当焦点在x轴上时,∵双曲线的渐近线方程为y=±2x,∴
| b |
| 2 |
∴方程为
| x2 |
| 4 |
| y2 |
| 16 |
当焦点在y轴上时,∵双曲线的渐近线方程为y=±2x,∴
| 2 |
| b |
∴方程为
| y2 |
| 4 |
故答案为:
| x2 |
| 4 |
| y2 |
| 16 |
| y2 |
| 4 |
点评:本题考查双曲线的标准方程与几何性质,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=ln(x+2)-
的零点所在区间为(k,k+1)(其中k为整数),则k的值为( )
| 1 |
| x |
| A、0 | B、1 | C、-2 | D、0或-2 |
双曲线上右支上存在点P,使得右焦点F关于直线OP的对称点在y轴上(O为坐标原点),则双曲线离心率的取值范围为( )
A、(
| ||||
B、(
| ||||
C、(1,
| ||||
D、(
|
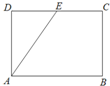
如图,在矩形ABCD中,AB=2,BC=
,E是CD的中点,那么
•
=( )
| 3 |
| AE |
| DC |

| A、4 | ||
| B、2 | ||
C、
| ||
| D、1 |
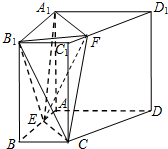 如图,在四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,∠BAD=90°,AD∥BC,且A1A=AB=AD=2BC=2,点E在棱AB上,平面A1EC与棱C1D1相交于点F.
如图,在四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,∠BAD=90°,AD∥BC,且A1A=AB=AD=2BC=2,点E在棱AB上,平面A1EC与棱C1D1相交于点F.