题目内容
| ∫ | 2π 0 |
| A、0 | B、2 | C、4 | D、2π |
考点：定积分
专题：导数的概念及应用
分析：根据积分的公式即可得到结论．
解答：
解：
|sinx|dx=2∫
sinxdx=2（-cosx）|
=4．
故选：C
| ∫ | 2π 0 |
π 0 |
π 0 |
故选：C
点评：本题主要考查积分的计算，要求熟练积分的公式和运算法则．
练习册系列答案
相关题目
在△ABC中，已知角A，B，C所对的边分别为a，b，c，且a=3，c=8，B=60°，则△ABC的周长是（ ）
| A、18 | B、19 | C、16 | D、17 |
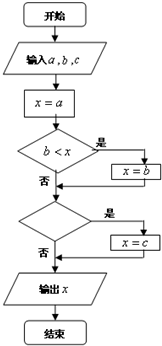如图所示程序框图中，如果输入三个实数a、b、c，要求输出这三个数中最小的数，那么在空白的判断框中，应该填入下面四个选项中的（ ）| A、c＜x | B、x＜c |
| C、c＜b | D、b＜c |
下列有关命题的说法正确的是（ ）
| A、命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1” |
| B、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
| C、命题“?x∈R，使得x2+x+1＜0”的否定是：“?x∈R，均有x2+x+1＜0” |
| D、命题“若x=y，则cosx=cosy”的逆否命题为真命题 |
设随机变量X是离散型随机变量，X∽B（n，p）且EX=1.6，DX=1.28，则数对X～B（n，p）的取值为 （ ）
| A、（8，0.2） |
| B、（5，0.32） |
| C、（7，0.45） |
| D、（4，0.4） |
