题目内容

若f（cosx）=cos3x，则f（sin
π
3
）的值为（　　）
A、-1
B、
3
2
C、0
D、1
考点：函数的值
专题：函数的性质及应用
分析：令cosx=sin
π
3
求出x的其中一个值，再代入函数解析式求解即可．
解答： 解：令cosx=sin
π
3
，则x的值可以取
π
6
，
所以f（sin
π
3
）=f（cos
π
6
）=cos
π
2
=0，
故选：C．
点评：本题考查复合函数的函数值，注意自变量的值，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=2
3
sin（
π
4
x）在同一半周期内的图象过点O，P，Q，其中O为坐标原点，P为函数图象的最高点，Q为函数f（x）的图象与x轴的正半轴的交点．
（1）试判断△OPQ的形状，并说明理由．
（2）若将△OPQ绕原点O按逆时针方向旋转角a（0＜a＜
π
2
）时，顶点P，Q，恰好同时落在曲线y=
k
x
（x＞0）上（如图所示），求实数k的值．
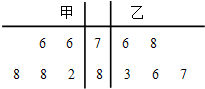甲、乙两名同学在5次体能测试中的成绩的茎叶图如图所示，设
.
x1
，
.
x2
分别表示甲、乙两名同学测试成绩的平均数，s1，s2分别表示甲、乙两名同学测试成绩的标准差，则有（　　）
A、
.
x1
=
.
x2
，s1＜s2
B、
.
x1
=
.
x2
，s1＞s2
C、
.
x1
＞
.
x2
，s1＞s2
D、
.
x1
=
.
x2
，s1=s2
设A、B、C是三角形的三个内角，下列关系恒成立的是（　　）
A、sin（A+B）=sinC
B、cos（A+B）=cosC
C、tan（A+B）=tanC
D、sin
A+B
2
=sin
C
2
对于给定的任意实数x，y，z（z≠0且z≠6），记xOy平面上点P（x，y）到三点A（z，z）、B（6-z，z-6）、C（0，0）的三个距离中的最大值为g（x，y，z），则g（x，y，z）的最小值是
 
．
定义在区间（0，+∞）上的函数f（x）若满足：（1）f（x）不恒为零；（2）对任意实数x，p，都有f（xp）=pf（x），我们就称f（x）为“降幂函数”
（1）判断y=log2x是否为“降幂函数”，并说明理由；
（2）若函数f（x）为“降幂函数”，证明：f（m•n）=f（n）+f（m）；
（3）若函数f（x）为“降幂函数”，且在（0，+∞）上单调递增，f（2）=1，f（x）满足f（m
1+sin2θ
+2sinθ•sin（θ+
π
3
）+cos2θ）-f（m）＞1对一切θ∈[0，
π
2
]上恒成立，求m的取值范围．
已知奇函数f（x）在x＞0时，f（x）=
1
3
x3-lnx，则f（x）在[-2，-
1
2
]上的值域为（　　）
A、[-ln2-
1
24
，-
1
3
]
B、[ln2-
8
3
，-ln2-
1
24
]
C、[ln2-
8
3
，-
1
3
]
D、[-
1
3
，ln2]
已知集合 A={2，-2}，B={x|x2-ax+4=0}，若A∪B=A，则实数a满足（　　）
A、{a|-4＜a＜4}
B、{a|-2＜a＜2}
C、{-4，4}
D、{a|-4≤a≤4}
已知椭圆T：
x2
a2
+
y2
b2
=1（a＞b＞0）经过点P（2，
2
），一个焦点F的坐标是（2，0）．
（1）求椭圆T的方程；
（2）设直线l：y=kx+m与椭圆T交于A、B两点，O为坐标原点，椭圆T的离心率为e，若kOA•kOB=e2-1，求证：△AOB的面积为定值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网