题目内容
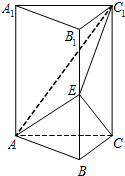 如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,CC1=
如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,CC1=| 2 |
(Ⅰ)求证:CE⊥AC1;
(Ⅱ)求二面角A-C1E-C的余弦值.
考点:用空间向量求平面间的夹角,直线与平面垂直的性质
专题:空间位置关系与距离,空间角,空间向量及应用
分析:(Ⅰ)根据已知条件,分别以AB,BC,BB1三条直线为x轴,y轴,z轴建立空间直角坐标系,根据已知的边的长度即可求出
,
的坐标,求数量积
•
=0即可;
(Ⅱ)分别求平面AEC1,平面C1EC的法向量,求两法向量的夹角的余弦值即可.容易判断出
=(-1,0,0)是平面C1EC的法向量,设平面AEC1的法向量为
=(x,y,z),根据
与向量
,
垂直,而向量
,
的坐标根据已知的边的长度可求出,所以可求出
的坐标,所以根据向量夹角的余弦的坐标公式即可求出这两法向量的夹角的余弦值,即求出了二面角E-AF-C的余弦值.
| CE |
| AC1 |
| CE |
| AC1 |
(Ⅱ)分别求平面AEC1,平面C1EC的法向量,求两法向量的夹角的余弦值即可.容易判断出
| BA |
| n |
| n |
| AC1 |
| AE |
| AC1 |
| AE |
| n |
解答:
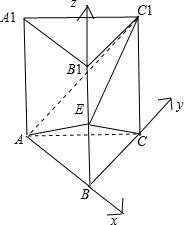 解:(Ⅰ)由已知条件知,AB,BC,BB1三条直线两两垂直,所以可分别以这三条直线为x轴,y轴,z轴建立如图所示空间直角坐标系;
解:(Ⅰ)由已知条件知,AB,BC,BB1三条直线两两垂直,所以可分别以这三条直线为x轴,y轴,z轴建立如图所示空间直角坐标系;
∴B(0,0,0),A(-1,0,0),E(0,0,
),C1(0,1,
),C(0,1,0);
∴
=(0,-1,
),
=(1,1,
);
∴
•
=0,∴
⊥
;
∴CE⊥AC1;
(Ⅱ)BA⊥平面C1EC,∴
=(-1,0,0)即为平面C1EC的一个法向量;
=(1,1,
),
=(1,0,
),设平面AEC1的法向量为
=(x,y,z),则
;
∴
,令z=1,则
=(-
,-
,1);
∴cos<
,
>=
=
=
,
∴二面角A-C1E-C的余弦值为
.
 解:(Ⅰ)由已知条件知,AB,BC,BB1三条直线两两垂直,所以可分别以这三条直线为x轴,y轴,z轴建立如图所示空间直角坐标系;
解:(Ⅰ)由已知条件知,AB,BC,BB1三条直线两两垂直,所以可分别以这三条直线为x轴,y轴,z轴建立如图所示空间直角坐标系;∴B(0,0,0),A(-1,0,0),E(0,0,
| ||
| 2 |
| 2 |
∴
| CE |
| ||
| 2 |
| AC1 |
| 2 |
∴
| CE |
| AC1 |
| CE |
| AC1 |
∴CE⊥AC1;
(Ⅱ)BA⊥平面C1EC,∴
| BA |
| AC1 |
| 2 |
| AE |
| ||
| 2 |
| n |
|
∴
|
| n |
| ||
| 2 |
| ||
| 2 |
∴cos<
| BA |
| n |
| ||||
|
|
| ||||
|
| 1 |
| 2 |
∴二面角A-C1E-C的余弦值为
| 1 |
| 2 |
点评:考查利用空间向量证明异面直线垂直,求二面角的问题,两向量垂直的充要条件,向量数量积的坐标运算,以及平面法向量的概念,向量夹角的余弦公式.

练习册系列答案
相关题目
已知集合A={x|-1≤x<3},B={x|2<x≤5},则A∩B=( )
| A、(2,3) |
| B、[-1,5] |
| C、(-1,5) |
| D、(-1,5] |
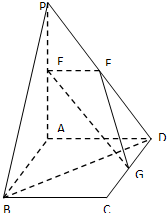 如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F,G分别是线段PA、PD、CD的中点.
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F,G分别是线段PA、PD、CD的中点.