题目内容
已知集合M={x|x2-3x≤10},N={x|a+1≤x≤2a+1}.
(1)若a=2,求M∩(CRN);
(2)若M∪N=M,求实数a的取值范围.
(1)若a=2,求M∩(CRN);
(2)若M∪N=M,求实数a的取值范围.
考点:并集及其运算,交、并、补集的混合运算
专题:集合
分析:(Ⅰ)a=2时,M={x|-2≤x≤5},N={3≤x≤5},由此能求出M∩(CRN).
(Ⅱ)由M∪N=M,得N?M,由此能求出实数a的取值范围.
(Ⅱ)由M∪N=M,得N?M,由此能求出实数a的取值范围.
解答:
(本小题满分8分)
解:(Ⅰ)a=2时,M={x|-2≤x≤5},N={3≤x≤5},
CRN={x|x<3或x>5},
所以M∩(CRN)={x|-2≤x<3}.
(Ⅱ)∵M∪N=M,∴N?M,
①a+1>2a+1,解得a<0;
②
,解得0≤a≤2.
所以a≤2.
解:(Ⅰ)a=2时,M={x|-2≤x≤5},N={3≤x≤5},
CRN={x|x<3或x>5},
所以M∩(CRN)={x|-2≤x<3}.
(Ⅱ)∵M∪N=M,∴N?M,
①a+1>2a+1,解得a<0;
②
|
所以a≤2.
点评:本题考查交集、实集的应用,考查实数的取值范围的求法,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
复数
在复平面上对应的点位于( )
| i |
| 3-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
“a>b”是“log2a>log2b”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设集合M={x|x+1>0},N={x|x-2<0},则M∩N=( )
| A、(-1,+∞) |
| B、[-1,2) |
| C、(-1,2) |
| D、[-1,2] |
如图所示是四棱锥的三视图,则该几何的体积等于( )
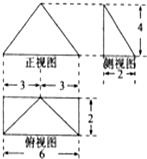

| A、16 | ||
B、34+6
| ||
| C、6 | ||
D、17+6
|
设集合P={3,log2a},Q={a,b},若P∩Q={0},则P∪Q=( )
| A、{3,0} |
| B、{3,1,0} |
| C、{3,2,0} |
| D、{3,2,1,0} |
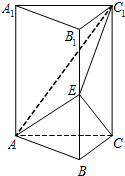 如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,CC1=
如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,CC1=