题目内容
已知数列{an}的前n项和Sn=n2+n+1,则a1+a9等于( )
| A、19 | B、20 | C、21 | D、22 |
考点:数列递推式
专题:等差数列与等比数列
分析:由已知得a1+a9=S1+S9-S8,由此能求出结果.
解答:
解:∵数列{an}的前n项和Sn=n2+n+1,
∴a1+a9=S1+S9-S8
=(1+1+1)+(81+9+1-64-8-1)
=21.
故选:C.
∴a1+a9=S1+S9-S8
=(1+1+1)+(81+9+1-64-8-1)
=21.
故选:C.
点评:本题考查数列的两项和的求法,是基础题,解题时要注意数列的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
复数Z满足(1+i)Z=|1-i|,是Z的虚部为( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
若函数f(x)=x•(x-c)2在x=2处有极大值,则常数c的值为( )
| A、6 | ||
| B、2 | ||
| C、2或6 | ||
D、
|
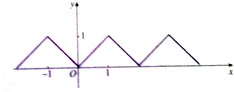 已知函数y=f(x)的图象如图所示,试回答下列问题:
已知函数y=f(x)的图象如图所示,试回答下列问题: