题目内容
16.已知$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-3,4),$\overrightarrow{c}$=$\overrightarrow{a}$+λ$\overrightarrow{b}$(λ∈R),当λ为何值时,$\overrightarrow{c}$与$\overrightarrow{a}$的夹角为45°?分析 利用夹角公式求出夹角余弦,列出方程解出.
解答 解:$\overrightarrow{c}$=(1-3λ,2+4λ),∴$\overrightarrow{a}•\overrightarrow{c}$=1-3λ+2(2+4λ)=5λ+5.|$\overrightarrow{a}$|=$\sqrt{5}$,|$\overrightarrow{c}$|=$\sqrt{(1-3λ)^{2}+(2+4λ)^{2}}$=$\sqrt{25{λ}^{2}+10λ+5}$.
∴cos45°=$\frac{\overrightarrow{a}•\overrightarrow{c}}{|\overrightarrow{a}|•|\overrightarrow{c}|}$=$\frac{5λ+5}{\sqrt{5}•\sqrt{25{λ}^{2}+10λ+5}}$=$\frac{\sqrt{2}}{2}$.解得λ=1,或λ=-$\frac{1}{3}$.
点评 本题考查了平面向量的数量积运算与夹角公式,是基础题.

练习册系列答案
相关题目
6.在空间中,已知动点P(x,y,z)满足z=0,则动点P的轨迹是( )
| A. | 平面 | B. | 直线 | ||
| C. | 不是平面,也不是直线 | D. | 以上都不对 |
4.设A(x1,a)、B(x2,a)是周期为2π的函数y=sin(ωx-$\frac{π}{3}$)(ω>0)图象上两点,且满足0<x1<x2<2π,0<a<1,则x1+x2=( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{5π}{6}$ | D. | $\frac{5π}{3}$ |
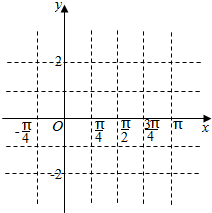 已知函数f(x)=2cosx•sin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinx•cosx.
已知函数f(x)=2cosx•sin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinx•cosx.