题目内容
4.设A(x1,a)、B(x2,a)是周期为2π的函数y=sin(ωx-$\frac{π}{3}$)(ω>0)图象上两点,且满足0<x1<x2<2π,0<a<1,则x1+x2=( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{5π}{6}$ | D. | $\frac{5π}{3}$ |
分析 根据函数的周期求出ω=1,进而分析出函数图象的对称轴方程,结合0<x1<x2<2π,0<a<1,可得:A,B两点关于直线x=$\frac{5π}{6}$对称,进而得到答案.
解答 解:∵函数y=sin(ωx-$\frac{π}{3}$)(ω>0)的周期为2π,且ω>0,
∴ω=1,
∴函数y=sin(x-$\frac{π}{3}$),
由x-$\frac{π}{3}$=$\frac{π}{2}$+kπ,k∈Z得:函数y=sin(x-$\frac{π}{3}$)图象的对称轴方程为:x=$\frac{5π}{6}$+kπ,k∈Z,
∵0<x1<x2<2π,0<a<1,
∴A,B两点关于直线x=$\frac{5π}{6}$对称,
∴x1+x2=$\frac{5π}{3}$,
故选:D.
点评 本题考查的知识点是正弦函数的图象和性质,熟练掌握正弦函数的图象和性质是解答的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
15.下列命题正确的是( )
| A. | y=sinx在[0,π]内是单调函数 | |
| B. | 在第二象限内,y=sinx是减函数,y=cosx也是减函数 | |
| C. | y=cosx的增区间是[0,π] | |
| D. | y=sinx在区间[$\frac{π}{2}$,π]上是减函数 |
12.函数f′(x)是奇函数f(x)(x∈R)的导函数,f(1)=0,当x<0时,xf′(x)+f(x)>0,则使得f(x)<0成立的x的取值范围是( )
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-1,0)∪(0,1) |
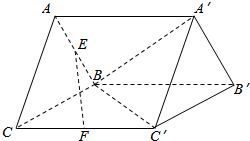 如图,三棱柱ABC-A′B′C′,BC=1,BC′=1,CC′=$\sqrt{2}$,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.
如图,三棱柱ABC-A′B′C′,BC=1,BC′=1,CC′=$\sqrt{2}$,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.