题目内容
7.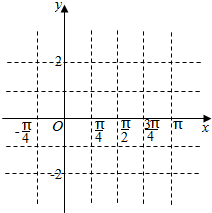 已知函数f(x)=2cosx•sin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinx•cosx.
已知函数f(x)=2cosx•sin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinx•cosx.(1)当x∈[0,$\frac{π}{2}$]时,求f(x)的值域;
(2)用五点法在图中作出y=f(x)在闭区间[-$\frac{π}{6}$,$\frac{5π}{6}$]上的简图;
(3)说明f(x)的图象可由y=sinx的图象经过怎样的变化得到?
分析 (1)由条件利用三角函数恒等变换的应用化简函数解析式可得f(x)=2sin(2x+$\frac{π}{3}$),由x∈[0,$\frac{π}{2}$]根据正弦函数的定义域和值域即可得解.
(2)用五点法作函数y=Asin(ωx+φ)在一个周期上的简图.
(3)根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:(1)∵f(x)=2cosx•sin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinx•cosx
=sin2x+$\sqrt{3}$cos2x
=2sin(2x+$\frac{π}{3}$),
∵x∈[0,$\frac{π}{2}$],2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{4π}{3}$],
∴f(x)=2sin(2x+$\frac{π}{3}$)∈[-$\sqrt{3}$,2].
(2)列表:
| 2x+$\frac{π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{6}$ | $\frac{π}{12}$ | $\frac{π}{3}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ |
| y | 0 | 2 | 0 | -2 | 0 |
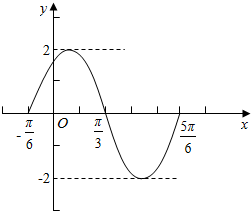
(3)把y=sinx的图象向左平移$\frac{π}{3}$个单位,可得函数y=sin(x+$\frac{π}{3}$)的图象;
再把所得图象上点的横坐标变为原来的$\frac{1}{2}$倍,可得函数y=sin(2x+$\frac{π}{3}$)的图象;
再把所得图象上的点的纵坐标变为原来的2倍,可得函数y=2sin(2x+$\frac{π}{3}$)的图象.
点评 本题主要考查正弦函数的定义域和值域,用五点法作函数y=Asin(ωx+φ)在一个周期上的简图,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
15.下列命题正确的是( )
| A. | y=sinx在[0,π]内是单调函数 | |
| B. | 在第二象限内,y=sinx是减函数,y=cosx也是减函数 | |
| C. | y=cosx的增区间是[0,π] | |
| D. | y=sinx在区间[$\frac{π}{2}$,π]上是减函数 |
12.函数f′(x)是奇函数f(x)(x∈R)的导函数,f(1)=0,当x<0时,xf′(x)+f(x)>0,则使得f(x)<0成立的x的取值范围是( )
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-1,0)∪(0,1) |
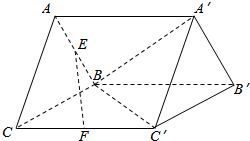 如图,三棱柱ABC-A′B′C′,BC=1,BC′=1,CC′=$\sqrt{2}$,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.
如图,三棱柱ABC-A′B′C′,BC=1,BC′=1,CC′=$\sqrt{2}$,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.