题目内容
给出以下四个命题:
①在△ABC中,“A<B”是“sinA<sinB”的必要不充分条件;
②函数f(x)=|sinx-cosx|的最小正周期是2π;
③在△ABC中,若AB=2
,AC=2
,B=
,则△ABC为钝角三角形;
④在同一坐标系中,函数y=sinx与函数y=lgx的图象有三个交点.
其中正确命题的序号是 .
①在△ABC中,“A<B”是“sinA<sinB”的必要不充分条件;
②函数f(x)=|sinx-cosx|的最小正周期是2π;
③在△ABC中,若AB=2
| 2 |
| 3 |
| π |
| 3 |
④在同一坐标系中,函数y=sinx与函数y=lgx的图象有三个交点.
其中正确命题的序号是
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:根据正弦定理及三角形大边对大角,可判断△ABC中,“A>B”与“sinA>sinB”的充要关系,可判断①;求出函数f(x)=|sinx-cosx|的最小正周期可判断②;利用正弦定理求解△ABC,可判断③;求出函数y=sinx与函数y=lgx的图象交点个数,可判断④.
解答:
解:在△ABC中,“A>B”?“a>b”?“sinA•2R>sinB•2R”(其中R为三角形外接圆半径)?“sinA>sinB”,故A>B”是“sinA>sinB”的充要条件,故①错误;
函数f(x)=|sinx-cosx|的最小正周期是π,故②错误;
由AB=2
,AC=2
,B=
,由正弦定理可得:A=
,则C=
,即△ABC为锐角三角形,故③错误;
作出函数y=lgx与函数y=sinx在[0,10]上的图象,如下图
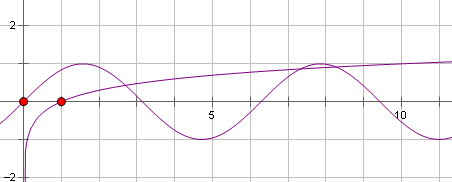
则图可知,有3个交点.故④正确;
故答案为:④
函数f(x)=|sinx-cosx|的最小正周期是π,故②错误;
由AB=2
| 2 |
| 3 |
| π |
| 3 |
| π |
| 4 |
| 5π |
| 12 |
作出函数y=lgx与函数y=sinx在[0,10]上的图象,如下图

则图可知,有3个交点.故④正确;
故答案为:④
点评:本题以命题的真假判断为载体,考查了充要条件,正弦定理,函数的周期性,函数图象,难度中档.

练习册系列答案
相关题目
已知定义在R上的偶函数f(x)在[0,+∞)上单调递增,且f(2)=0,则不等式f(log2x)>0的解集为( )
A、(
| ||
B、(-∞,
| ||
C、(0,
| ||
D、(-∞,
|
与函数y=2x-1相等的函数是( )
| A、y=2|x|-1 | |||
B、y=
| |||
C、y=2
| |||
D、y=2(
|
已知x>0,y>0,z>0,x-y+2z=0则
的( )
| xz |
| y2 |
| A、最小值为8 | ||
| B、最大值为8 | ||
C、最小值为
| ||
D、最大值为
|
角α终边上一点P的坐标为(1-t,t),其中t∈[-1,1)∪(1,2],那么tanα的取值范围为( )
A、(-∞,-2]∪[-
| ||
B、[-2,-
| ||
C、[-2,0)∪(0,-
| ||
D、[-2,-1)∪(-1,-
|