题目内容
19.若$acos({π-A})+bsin({\frac{π}{2}+B})=0$,内角A,B的对边分别为a,b,则三角形ABC的形状为等腰三角形或直角三角形.分析 用诱导公式化简已知,利用正弦定理将acosA=bcosB中等号两边的边转化为该边所对角的正弦,化简整理即可.
解答 解:∵在△ABC中,acos(π-A)+bsin($\frac{π}{2}$+B)=0,
∴acosA=bcosB,
∴由正弦定理得:a=2RsinA,b=2RsinB,
∴sinAcosA=sinBcosB,
∴$\frac{1}{2}$sin2A=$\frac{1}{2}$sin2B,
∴sin2A=sin2B,
∴2A=2B或2A=π-2B,
∴A=B或A+B=$\frac{π}{2}$,
∴△ABC为等腰或直角三角形,
故答案为:等腰三角形或直角三角形
点评 本题考查三角形的形状判断,着重考查正弦定理与二倍角的正弦的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知-9,a1,a2,-1成等差数列,-9,b1,b2,b3,-1成等比数列,则b2(a1+a2)等于( )
| A. | 30 | B. | -30 | C. | ±30 | D. | 15 |
11. 2014年某大学自主招生面试环节中,七位评委为一考生打出分数的茎叶图如图21,去掉一个最高分和一个最低分,所剩数据的平均数,众数和中位数分别为( )
2014年某大学自主招生面试环节中,七位评委为一考生打出分数的茎叶图如图21,去掉一个最高分和一个最低分,所剩数据的平均数,众数和中位数分别为( )
 2014年某大学自主招生面试环节中,七位评委为一考生打出分数的茎叶图如图21,去掉一个最高分和一个最低分,所剩数据的平均数,众数和中位数分别为( )
2014年某大学自主招生面试环节中,七位评委为一考生打出分数的茎叶图如图21,去掉一个最高分和一个最低分,所剩数据的平均数,众数和中位数分别为( )| A. | 84,84,86 | B. | 84,84,84 | C. | 85,84,86 | D. | 85,84,84 |
8.设函数f(x)的定义域为D,如果存在正实数k,使对任意x∈D,都有x+k∈D,且f(x+k)>f(x)恒成立,则称函数f(x)为D上的“k型增函数”.已知f(x)是定义在R上的奇函数,且当x>0时,f(x)=|x-a|-2a,若f(x)为R上的“2 015型增函数”,则实数a的取值范围是( )
| A. | (-∞,$\frac{2015}{4}$) | B. | ($\frac{2015}{4}$,+∞) | C. | (-∞,$\frac{2015}{6}$) | D. | ($\frac{2015}{6}$,+∞) |
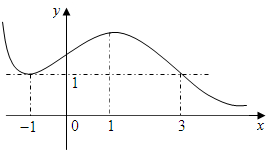 f′(x)为定义在R上的函数f(x)的导函数,而y=3f'(x)的图象如图所示,则y=f(x)的单调递增区间是(-∞,3].
f′(x)为定义在R上的函数f(x)的导函数,而y=3f'(x)的图象如图所示,则y=f(x)的单调递增区间是(-∞,3].