题目内容
7.已知f(x)=x3-3x,并设:p:?c∈R,f(f(x))=c至少有3个实根;
q:当c∈(-2,2)时,方程f(f(x))=c有9个实根;
r:当c=2时,方程f(f(x))=c有5个实根.
则下列命题为真命题的是( )
| A. | ¬p∨¬r | B. | ¬q∧r | C. | 仅有r | D. | p∧q |
分析 求出f(x)的导数和单调区间、极值,画出图象,令t=f(x),f(t)=c,讨论c的范围,结合函数f(x)的图象判断p假,q,r为真,再由复合命题的真假判断,即可得到答案.
解答 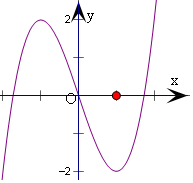 解:f(x)=x3-3x的导数为f′(x)=3x2-3,
解:f(x)=x3-3x的导数为f′(x)=3x2-3,
当x>1或x<-1时,f′(x)>0,f(x)递增;
当-1<x<1时,f′(x)<0,f(x)递减.
可得f(-1)=2取得极大值,f(1)取得极小值-2.
作出y=f(x)的图象(如右):
令t=f(x),
对于p:?c∈R,f(f(x))=c至少有3个实根,
即有f(t)=c,若c>2,则t>2,此时f(x)=t只有一解,故p为假命题;
对于q:当c∈(-2,2)时,方程f(f(x))=c有9个实根,
由t=f(x),f(t)=c在(-2,2)内有三个解,在x轴上方不妨设-$\sqrt{3}$<t1<-1<t2<0<1<t3<2,
由图象可得f(x)=t共有9个实根,故q为真命题;
对于r:当c=2时,方程f(f(x))=c有5个实根,
由t=f(x),f(t)=2,可得t=-1和2,
由图象可得f(x)=-1有3个实根,f(x)=2有2个实根,共有5个实根.故r为真命题.
则¬p∨¬r为真命题;¬q∧r,仅有r,p∧q均为假命题.
故选:A.
点评 本题考查命题的真假判断,主要是考查函数的单调性和极值,以及换元思想和数形结合思想,考查复合命题的真假,以及判断能力,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
18.已知实数2,m,$\frac{9}{2}$依次构成一个等比数列,则圆锥曲线x2+$\frac{{y}^{2}}{m}$=1的离心率为( )
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{3}$或2 | D. | $\frac{2\sqrt{3}}{3}$或2 |
15.已知函数$f(x)=\left\{\begin{array}{l}1-{log_a}(x+2),x≥0\\ g(x),x<0\end{array}\right.$是奇函数,则方程g(x)=2的根为( )
| A. | $-\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | 6 | D. | -6 |
16.在等比数列{an}中,a1=1,a4=8,则a7=( )
| A. | 64 | B. | 32 | C. | 16 | D. | 12 |
17.已知i为虚数单位,则复数$\frac{1+i}{2i}$=( )
| A. | $\frac{1}{2}$+$\frac{1}{2}$i | B. | $\frac{1}{2}$-$\frac{1}{2}$i | C. | -$\frac{1}{2}$+$\frac{1}{2}$i | D. | -$\frac{1}{2}$-$\frac{1}{2}$i |