题目内容
12.已知函数f(x)=|x+a|+|x+$\frac{1}{a}$|(a>0)(a<0)(1)当a=2时,求不等式f(x)>3的解集
(2)证明:$f(m)+f(-\frac{1}{m})≥4$.
分析 (1)分类讨论,解不等式,即可得出结论;
(2)f(m)+f(-$\frac{1}{m}$)=|m+a|+|m+$\frac{1}{a}$|+|-$\frac{1}{m}$+a|+|-$\frac{1}{m}$+$\frac{1}{a}$|,利用三角不等式,及基本不等式即可证明结论.
解答 解:(1)当a=2时,f(x)=|x+2|+|x+$\frac{1}{2}$|,原不等式等价于$\left\{\begin{array}{l}{x<-2}\\{-x-2-x-\frac{1}{2}>3}\end{array}\right.$
或$\left\{\begin{array}{l}{-2≤x≤-\frac{1}{2}}\\{x+2-x-\frac{1}{2}>3}\end{array}\right.$或$\left\{\begin{array}{l}{x>\frac{1}{2}}\\{x+2+x+\frac{1}{2}>3}\end{array}\right.$
解得:x<-$\frac{11}{4}$或x∈∅或$x>\frac{1}{4}$,所以不等式的解集为{x|x<-$\frac{11}{4}$或$x>\frac{1}{4}\}$…(5分)
(2)f(m)+f(-$\frac{1}{m}$)=|m+a|+|m+$\frac{1}{a}$|+|-$\frac{1}{m}$+a|+|-$\frac{1}{m}$+$\frac{1}{a}$|
=$|m+a|+|-\frac{1}{m}+a|+|m+\frac{1}{a}|+|-\frac{1}{m}+\frac{1}{a}|≥2|m+\frac{1}{m}|=2(|m|+|\frac{1}{m}|)≥4$…(10分)
点评 本题考查绝对值不等式的解法,考查三角不等式,及基本不等式,属于中档题.

| A. | f(2a-x1)<f(2a-x2) | B. | f(2a-x1)>f(2a-x2) | C. | f(2a-x1)=f(2a-x2) | D. | 以上都不正确 |
p:?c∈R,f(f(x))=c至少有3个实根;
q:当c∈(-2,2)时,方程f(f(x))=c有9个实根;
r:当c=2时,方程f(f(x))=c有5个实根.
则下列命题为真命题的是( )
| A. | ¬p∨¬r | B. | ¬q∧r | C. | 仅有r | D. | p∧q |
| A. | x=$\frac{π}{3}$ | B. | x=$\frac{π}{6}$ | C. | x=-$\frac{π}{6}$ | D. | x=-$\frac{π}{3}$ |
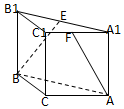 如图,ABC-A1B1C1是直三棱柱,∠BCA=90°,点E、F分别是A1B1、A1C1的中点,若BC=CA=AA1,则BE与AF所成角的余弦值为$\frac{\sqrt{30}}{10}$.
如图,ABC-A1B1C1是直三棱柱,∠BCA=90°,点E、F分别是A1B1、A1C1的中点,若BC=CA=AA1,则BE与AF所成角的余弦值为$\frac{\sqrt{30}}{10}$.