题目内容
16.在等比数列{an}中,a1=1,a4=8,则a7=( )| A. | 64 | B. | 32 | C. | 16 | D. | 12 |
分析 利用等比数列的通项公式求出公比,由此能求出a7的值.
解答 解:∵在等比数列{an}中,a1=1,a4=8,
∴${a}_{4}={a}_{1}{q}^{3}$,即8=q3,解得q=2,
a7=${a}_{1}{q}^{6}$=1×26=64.
故选:A.
点评 本题考查等比数列的第7项的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
6.随着教育制度和高考考试制度的改革,高校选拔人才的方式越来越多.某高校向一基地 学校投放了一个保送生名额,先由该基地学校初选出10名优秀学生,然后参与高校设置的 考核,考核设置了难度不同的甲、乙两个方案,每个方案都有M(文化)、N(面试)两个考核内 容,最终选择考核成绩总分第一名的同学定为该高校在基地校的保送生.假设每位同学完成 每个方案中的M、N两个考核内容的得分是相互独立的.根据考核前的估计,某同学完成甲 方案和乙方案的M、N两个考核内容的情况如表:
表1:甲方案
表2:乙方案
已知该同学最后一个参与考核,之前的9位同学的最高得分为125分.
(I)若该同学希望获得保送资格,应该选择哪个方案?请说明理由,并求其在该方案下 获得保送资格的概率;
(II)若该同学选用乙方案,求其所得成绩X的分布列及其数学期望EX.
表1:甲方案
| 考核内容 | M(文化) | N(面试) | ||
| 得分 | 100 | 80 | 50 | 20 |
| 概率 | $\frac{3}{4}$ | $\frac{1}{4}$ | $\frac{3}{4}$ | $\frac{1}{4}$ |
| 考核内容 | M(文化) | N(面试) | ||
| 得分 | 90 | 60 | 30 | 10 |
| 概率 | $\frac{9}{10}$ | $\frac{1}{10}$ | $\frac{9}{10}$ | $\frac{1}{10}$ |
(I)若该同学希望获得保送资格,应该选择哪个方案?请说明理由,并求其在该方案下 获得保送资格的概率;
(II)若该同学选用乙方案,求其所得成绩X的分布列及其数学期望EX.
7.已知f(x)=x3-3x,并设:
p:?c∈R,f(f(x))=c至少有3个实根;
q:当c∈(-2,2)时,方程f(f(x))=c有9个实根;
r:当c=2时,方程f(f(x))=c有5个实根.
则下列命题为真命题的是( )
p:?c∈R,f(f(x))=c至少有3个实根;
q:当c∈(-2,2)时,方程f(f(x))=c有9个实根;
r:当c=2时,方程f(f(x))=c有5个实根.
则下列命题为真命题的是( )
| A. | ¬p∨¬r | B. | ¬q∧r | C. | 仅有r | D. | p∧q |
4.如图P为平行四边形ABCD所在平面外一点,Q为PA的中点,O为AC与BD的交点,下面说法错误的是( ) 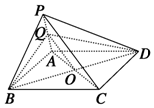

| A. | OQ∥平面PCD | B. | PC∥平面BDQ | C. | AQ∥平面PCD | D. | CD∥平面PAB |
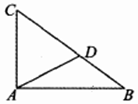 如图,在△ABC中,∠BAC=90°,点D为斜边BC上一点,且AC=CD=2.
如图,在△ABC中,∠BAC=90°,点D为斜边BC上一点,且AC=CD=2.