题目内容
15.已知函数$f(x)=\left\{\begin{array}{l}1-{log_a}(x+2),x≥0\\ g(x),x<0\end{array}\right.$是奇函数,则方程g(x)=2的根为( )| A. | $-\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | 6 | D. | -6 |
分析 利用奇函数的性质求出g(x),再解方程g(x)=2即可.
解答 解:设x<0,则f(-x)=1-loga(2-x),
∵f(x)是奇函数,∴f(x)=g(x)=-f(-x)=loga(2-x)-1,
又f(0)=0,∴1-loga2=0,∴a=2.
∴g(x)=log2(2-x)-1,
令g(x)=2得log2(2-x)=3,
解得x=-6.
故选D.
点评 本题考查了函数奇偶性的性质,对数的运算,属于中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
6.随着教育制度和高考考试制度的改革,高校选拔人才的方式越来越多.某高校向一基地 学校投放了一个保送生名额,先由该基地学校初选出10名优秀学生,然后参与高校设置的 考核,考核设置了难度不同的甲、乙两个方案,每个方案都有M(文化)、N(面试)两个考核内 容,最终选择考核成绩总分第一名的同学定为该高校在基地校的保送生.假设每位同学完成 每个方案中的M、N两个考核内容的得分是相互独立的.根据考核前的估计,某同学完成甲 方案和乙方案的M、N两个考核内容的情况如表:
表1:甲方案
表2:乙方案
已知该同学最后一个参与考核,之前的9位同学的最高得分为125分.
(I)若该同学希望获得保送资格,应该选择哪个方案?请说明理由,并求其在该方案下 获得保送资格的概率;
(II)若该同学选用乙方案,求其所得成绩X的分布列及其数学期望EX.
表1:甲方案
| 考核内容 | M(文化) | N(面试) | ||
| 得分 | 100 | 80 | 50 | 20 |
| 概率 | $\frac{3}{4}$ | $\frac{1}{4}$ | $\frac{3}{4}$ | $\frac{1}{4}$ |
| 考核内容 | M(文化) | N(面试) | ||
| 得分 | 90 | 60 | 30 | 10 |
| 概率 | $\frac{9}{10}$ | $\frac{1}{10}$ | $\frac{9}{10}$ | $\frac{1}{10}$ |
(I)若该同学希望获得保送资格,应该选择哪个方案?请说明理由,并求其在该方案下 获得保送资格的概率;
(II)若该同学选用乙方案,求其所得成绩X的分布列及其数学期望EX.
10.已知函数$f(x)=\frac{1}{3}m{x^3}+\frac{1}{2}n{x^2}+x+2017$,其中m∈{2,4,6,8},n∈{1,3,5,7},从这些函数中任取不同的两个函数,在它们在(1,f(1))处的切线相互平行的概率是( )
| A. | $\frac{7}{120}$ | B. | $\frac{7}{60}$ | C. | $\frac{7}{30}$ | D. | 以上都不对 |
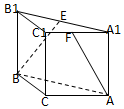 如图,ABC-A1B1C1是直三棱柱,∠BCA=90°,点E、F分别是A1B1、A1C1的中点,若BC=CA=AA1,则BE与AF所成角的余弦值为$\frac{\sqrt{30}}{10}$.
如图,ABC-A1B1C1是直三棱柱,∠BCA=90°,点E、F分别是A1B1、A1C1的中点,若BC=CA=AA1,则BE与AF所成角的余弦值为$\frac{\sqrt{30}}{10}$.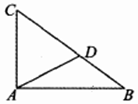 如图,在△ABC中,∠BAC=90°,点D为斜边BC上一点,且AC=CD=2.
如图,在△ABC中,∠BAC=90°,点D为斜边BC上一点,且AC=CD=2.