题目内容
已知正项等差数列{an}满足：an2-an+1-an-1=0（n≥2），等比数列{bn}满足：bn+1•bn-1-2bn=0（n≥2），则log2（an+bn）=（ ）
| A、-1或2 | B、0或2 | C、1 | D、2 |
考点：数列递推式
专题：等差数列与等比数列
分析：根据数列的递推关系，结合等差和等比数列的定义和性质求出数列的通项公式即可得到结论．
解答：
解：由an2-an+1-an-1=0（n≥2），得an2=an+1+an-1，
∵{an}是正项等差数列，
∴an2=an+1+an-1=2an，
∴an=2，（n≥2），
∵bn+1•bn-1-2bn=0（n≥2），
∴bn+1•bn-1=2bn（n≥2），
∵{bn}是等比数列，
∴bn+1•bn-1=bn2=2bn（n≥2），
∴bn=2，（n≥2），
则log2（an+bn）=log2（2+2）=log24=2，
故选：D．
∵{an}是正项等差数列，
∴an2=an+1+an-1=2an，
∴an=2，（n≥2），
∵bn+1•bn-1-2bn=0（n≥2），
∴bn+1•bn-1=2bn（n≥2），
∵{bn}是等比数列，
∴bn+1•bn-1=bn2=2bn（n≥2），
∴bn=2，（n≥2），
则log2（an+bn）=log2（2+2）=log24=2，
故选：D．
点评：本题主要考查对数的基本运算，根据等差数列和等比数列的性质，求出数列的通项公式是解决本题的关键．
练习册系列答案
相关题目
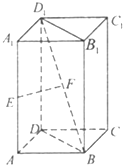如图，已知棱柱ABCD-A1B1C1D1的底面是正方形，且AA1⊥平面ABCD，E为棱AA1的中点，F为线段BD1的中点．
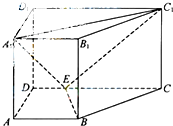如图，直四棱柱ABC-A1B1C1D1中，AB∥CD，AD⊥AB，AB=2，AD=对于函数y=sin（2x-
），下列说法正确的是（ ）
| π |
| 6 |
A、函数图象关于点（
| ||||
B、函数图象关于直线x=
| ||||
C、将它的图象向左平移
| ||||
D、将它的图象上各点的横坐标缩小为原来的
|