题目内容
| ∫ | 1 -1 |
考点:定积分
专题:导数的概念及应用
分析:
e|x|dx转化为
exdx+
e-xdx,根据定积分计算法则计算即可.
| ∫ | 1 -1 |
| ∫ | 1 0 |
| ∫ | 0 -1 |
解答:
解:
e|x|dx=
exdx+
e-xdx=ex|
-e-x|
=e-1-(1-e)=2e-2,
故答案为:2e-2.
| ∫ | 1 -1 |
| ∫ | 1 0 |
| ∫ | 0 -1 |
1 0 |
0 -1 |
故答案为:2e-2.
点评:本题考查了定积分的计算,属于基础题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
已知正项等差数列{an}满足:an2-an+1-an-1=0(n≥2),等比数列{bn}满足:bn+1•bn-1-2bn=0(n≥2),则log2(an+bn)=( )
| A、-1或2 | B、0或2 | C、1 | D、2 |
从1,2,3,4,5这5个数中任取两数,其中:①恰有一个是偶数和恰有一个是奇数;②至少有一个是奇数和两个都是奇数;③至少有一个是奇数和两个都是偶数;④至少有一个是奇数和至少有一个是偶数. 上述事件中,是对立事件的是( )
| A、① | B、②④ | C、③ | D、①③ |
 高三年上学期期末考试中,某班级数学成绩的频率分布直方图如图所示,数据分组依次如下:[70,90),[90,110),[100,130),[130,150),估计该班级数学成绩的平均分等于( )
高三年上学期期末考试中,某班级数学成绩的频率分布直方图如图所示,数据分组依次如下:[70,90),[90,110),[100,130),[130,150),估计该班级数学成绩的平均分等于( )| A、112 | B、114 |
| C、116 | D、120 |
已知某几何体的三视图如图所示,则该几何体的体积为( )
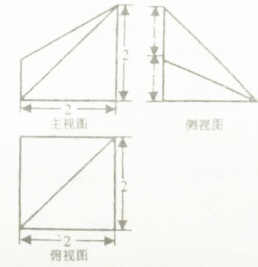

A、
| ||||
| B、8 | ||||
C、
| ||||
D、
|
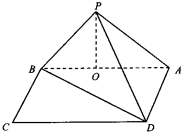 如图,在矩形ABCD中,AB=3
如图,在矩形ABCD中,AB=3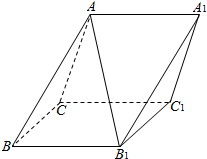 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2.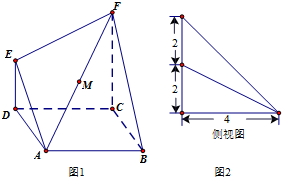 在如图1所示的多面体ABCDEF中,四边形ABCD是正方形,ED⊥平面ABCD,ED∥FC,ED=
在如图1所示的多面体ABCDEF中,四边形ABCD是正方形,ED⊥平面ABCD,ED∥FC,ED=