题目内容
已知函数f(x)=x+
,其中a∈R.
(Ⅰ)若f(x)为奇函数,求a的值;
(Ⅱ)当a=1时,判断函数f(x)在(1,
]上的单调性,并用定义证明你的结论;
(Ⅲ)证明:当θ∈(0,
)时,sinθ+cosθ+
的最小值为3
+2.
| 2 |
| x-a |
(Ⅰ)若f(x)为奇函数,求a的值;
(Ⅱ)当a=1时,判断函数f(x)在(1,
| 2 |
(Ⅲ)证明:当θ∈(0,
| π |
| 2 |
| 1+sinθ+cosθ |
| sinθcosθ |
| 2 |
考点:函数单调性的判断与证明,函数奇偶性的判断
专题:综合题,函数的性质及应用
分析:(Ⅰ)由函数f(x)为奇函数,得f(-x)+f(x)=0,求出a的值;
(Ⅱ)a=1时,函数f(x)=x+
在(1,
]上是减函数,用定义证明即可;
(Ⅲ)构造函数,设sinθ+cosθ=t,则1<t≤
,sinθ+cosθ+
=t+
;
由f(t)=t+
在区间(1,
]上的单调性,求出f(t)的最小值.
(Ⅱ)a=1时,函数f(x)=x+
| 2 |
| x-1 |
| 2 |
(Ⅲ)构造函数,设sinθ+cosθ=t,则1<t≤
| 2 |
| 1+sinθ+cosθ |
| sinθcosθ |
| 2 |
| t-1 |
由f(t)=t+
| 2 |
| t-1 |
| 2 |
解答:
解:(Ⅰ)∵函数f(x)=x+
为奇函数,其中a∈R;
∴f(-x)+f(x)=(-x+
)+(x+
)=0,
∴
=
,
∴a=0;
(Ⅱ)a=1时,函数f(x)=x+
在(1,
]上是减函数,
用定义证明x1、x2∈(1,
],且x1<x2;
则f(x1)-f(x2)=(x1+
)-(x2+
)
=(x1-x2)[1-
],
∵1<x1<x2≤
,∴x1-x2<0;
∴(x1-1)(x2-1)<(
)2-1=1,
∴1-
<0;
∴f(x1)-f(x2)>0,
即f(x1)>f(x2);
∴f(x)是减函数;
(Ⅲ)证明:设sinθ+cosθ=t,∴t=
sin(θ+
),
当θ∈(0,
)时,
<sin(θ+
)≤1,∴1<t≤
;
∵t2=1-2sinθcosθ,
∴sinθcosθ=
;
∴sinθ+cosθ+
=t+
=t+
;
又∵f(t)=t+
在区间(1,
]上是减函数,
∴当t=
时,f(t)取得最小值为3
+2.
| 2 |
| x-a |
∴f(-x)+f(x)=(-x+
| 2 |
| -x-a |
| 2 |
| x-a |
∴
| 2 |
| x+a |
| 2 |
| x-a |
∴a=0;
(Ⅱ)a=1时,函数f(x)=x+
| 2 |
| x-1 |
| 2 |
用定义证明x1、x2∈(1,
| 2 |
则f(x1)-f(x2)=(x1+
| 2 |
| x1-1 |
| 2 |
| x2-1 |
=(x1-x2)[1-
| 2 |
| (x1-1)(x2-1) |
∵1<x1<x2≤
| 2 |
∴(x1-1)(x2-1)<(
| 2 |
∴1-
| 2 |
| (x1-1)(x2-1) |
∴f(x1)-f(x2)>0,
即f(x1)>f(x2);
∴f(x)是减函数;
(Ⅲ)证明:设sinθ+cosθ=t,∴t=
| 2 |
| π |
| 4 |
当θ∈(0,
| π |
| 2 |
| ||
| 2 |
| π |
| 4 |
| 2 |
∵t2=1-2sinθcosθ,
∴sinθcosθ=
| t2-1 |
| 2 |
∴sinθ+cosθ+
| 1+sinθ+cosθ |
| sinθcosθ |
| 1+t | ||
|
| 2 |
| t-1 |
又∵f(t)=t+
| 2 |
| t-1 |
| 2 |
∴当t=
| 2 |
| 2 |
点评:本题考查了函数的奇偶性,单调性的证明以及应用问题,解题时用定义来证明函数的单调性,应用构造函数的方法,结合函数的单调性求最值问题,是综合题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
阅读如图所示的程序框图,则输出的S的值为( )


A、-
| ||||
| B、0 | ||||
C、
| ||||
D、
|

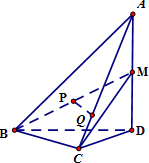 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.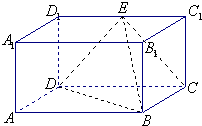 长方体ABCD-A1B1C1D1的侧棱AA1=a,AB=2a,AA1=BC=a的矩形,E为C1D1的中点.
长方体ABCD-A1B1C1D1的侧棱AA1=a,AB=2a,AA1=BC=a的矩形,E为C1D1的中点. 如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.
如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.