题目内容
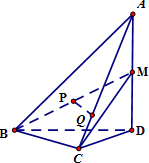 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.(1)证明:PQ∥平面BCD;
(2)若异面直线PQ与CD所成的角为45°,二面角C-BM-D的大小为θ,求cosθ的值.
考点:与二面角有关的立体几何综合题,异面直线及其所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)连AP并延长交BD于E,连CE,过M作MN∥BD交AP于N,由已知条件推导出PQ∥CE.由此能证明PQ∥平面BCD.
(2)过C作CF⊥BD于F,作CR⊥BM于R,连FR.由已知条件推导出∠CRF=θ即为二面角C-BM-D的平面角,由此能求出cosθ的值.
(2)过C作CF⊥BD于F,作CR⊥BM于R,连FR.由已知条件推导出∠CRF=θ即为二面角C-BM-D的平面角,由此能求出cosθ的值.
解答:
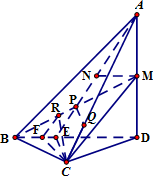 (1)证明:如图,连AP并延长交BD于E,连CE,
(1)证明:如图,连AP并延长交BD于E,连CE,
过M作MN∥BD交AP于N,则AN=NE,NP=PE.
故AP=3PE,从而PQ∥CE.
因PQ?平面BCD,CE?平面BCD,
故PQ∥平面BCD.
(2)解:过C作CF⊥BD于F,作CR⊥BM于R,连FR.
因AD⊥平面BCD,故平面ABD⊥平面BCD,
故CF⊥平面ABD,因此CF⊥BM,从而BM⊥平面RCF,
所以∠CRF=θ即为二面角C-BM-D的平面角.
因PQ∥CE,故∠DCE=45°,因此CE即为∠BCD的角平分线.
由 (1)知DE=2MN=2EB,故DC=2BC,
从而BC=1,CF=
=
.
由题意知BC⊥平面ACD,故BC⊥CM.
由题意知CM=2
,故CR=
=
.
所以sinθ=
=
,从而cosθ=
=
.
 (1)证明:如图,连AP并延长交BD于E,连CE,
(1)证明:如图,连AP并延长交BD于E,连CE,过M作MN∥BD交AP于N,则AN=NE,NP=PE.
故AP=3PE,从而PQ∥CE.
因PQ?平面BCD,CE?平面BCD,
故PQ∥平面BCD.
(2)解:过C作CF⊥BD于F,作CR⊥BM于R,连FR.
因AD⊥平面BCD,故平面ABD⊥平面BCD,
故CF⊥平面ABD,因此CF⊥BM,从而BM⊥平面RCF,
所以∠CRF=θ即为二面角C-BM-D的平面角.
因PQ∥CE,故∠DCE=45°,因此CE即为∠BCD的角平分线.
由 (1)知DE=2MN=2EB,故DC=2BC,
从而BC=1,CF=
| 1•2 | ||
|
| 2 | ||
|
由题意知BC⊥平面ACD,故BC⊥CM.
由题意知CM=2
| 2 |
1•2
| ||
|
2
| ||
| 3 |
所以sinθ=
| CF |
| CR |
| 3 | ||
|
| 1 | ||
|
| ||
| 10 |
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
下列函数中,既是奇函数,又是减函数的是( )
A、y=x
| ||
| B、y=2|x| | ||
C、y=
| ||
| D、y=2-x-2x |
圆内接四边形ABCD中,∠A,∠B,∠C的度数的比是3:4:6,则∠D=( )
| A、60° | B、80° |
| C、120° | D、100° |
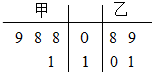 甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示.
甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示. 已知变量x,y满足
已知变量x,y满足