题目内容

设实数x、y满足
x≥0
x-2y≥0
x-y-2≤0
，则2x+y的最大值为
 
．
考点：简单线性规划
专题：不等式的解法及应用
分析：作出可行域，变形目标函数为y=-2x+z，平移直线可得结论．
解答： 解：作出
x≥0
x-2y≥0
x-y-2≤0
所对应的可行域，（如图阴影），
目标函数z=2x+y可化为y=-2x+z，可看作斜率为-2的直线，
平移直线可知，当直线经过直线x-2y=0和x-y-2=0的交点（4，2）时，
z=2x+y取最大值10，
∴2x+y的最大值为10
故答案为：10．
点评：本题考查简单线性规划，准确作图是解决问题的关键，属中档题．
练习册系列答案
相关题目
关于复数z=1+
1
(1+i)2
（i是虚数单位），下列表述正确的是（　　）
A、z是纯虚数
B、z是实数
C、z的虚部是1
D、在复平面内z对应的点在第四象限
执行如图所示的程序框图，若输出的结果为35，则判断框中应填（　　）
A、n≤5？B、n＞5？
C、n≤4？D、n＞4？
已知函数f（x）=x+
2
x-a
，其中a∈R．
（Ⅰ）若f（x）为奇函数，求a的值；
（Ⅱ）当a=1时，判断函数f（x）在（1，
2
]上的单调性，并用定义证明你的结论；
（Ⅲ）证明：当θ∈（0，
π
2
）时，sinθ+cosθ+
1+sinθ+cosθ
sinθcosθ
的最小值为3
2
+2．
解不等式：（m2+1）x2-4x+1≥0（m∈R）．
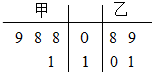甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示．
（Ⅰ）分别计算甲、乙训练得分的平均数和方差，并指出谁的训练成绩更好，为什么？
（Ⅱ）从甲、乙两名运动的训练成绩中各随机抽取1次的得分，分别记为x，y，设ξ=|x-8|+|y-10|，分别求出ξ取得最大值和最小值时的概率．
函数f（x）=Asin（ωx-
π
6
）+1（A＞0，ω＞0）的最大值为3，其图象相邻两条对称轴之间的而距离为
π
2
．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）用五点作图法画出函数f（x）在一个周期内的图象．
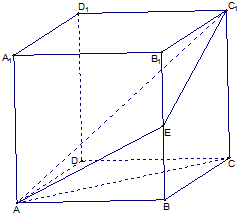正方体AC1中AB=2，E为BB1的中点．
（1）请在线段DD1上确定一点F使A，E，C1，F四点共面，并加以证明；
（2）求二面角C-AC1-E的平面角α的余弦值；
（3）点M在面ABCD内，且点M在平面AEC1F上的射影恰为△AEC1的重心，求异面直线AC与MC1所成角的余弦值．
在△ABC中，a、b、c分别为角A、B、C所对的边，且
3
c=2bsinC
（Ⅰ）试确定角B的大小；
（Ⅱ）若△ABC为锐角三角形，b=
3
，求a+c的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网