题目内容
f(x)=lg
,定义域[-9,9],在定义域内为奇函数,a∈R,
(1)求a的值;
(2)判断f(x)单调性并证明.
| a-x |
| 10+x |
(1)求a的值;
(2)判断f(x)单调性并证明.
考点:函数奇偶性的性质,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)根据奇函数的性质:f(0)=0,列出方程求出a的值.
(2)利用函数单调性的定义判断,先利用作差法证明对应真数的大小,根据对数函数的单调性得f(x1)与f(x2)的大小,即可得在定义域上的单调性.
(2)利用函数单调性的定义判断,先利用作差法证明对应真数的大小,根据对数函数的单调性得f(x1)与f(x2)的大小,即可得在定义域上的单调性.
解答:
解:(1)因为f(x)=lg
在定义域[-9,9]为奇函数,
所以f(0)=lg
=0,解得a=10,
则a的值是10;
(2)由(1)得,f(x)=lg
,定义域为[-9,9],
函数f(x)在定义域上单调递减,证明如下:
任取x1,x2∈[-9,9],且x1<x2,
则
-
=
=
因为-9≤x1<x2≤9,所以x2-x1>0,
则
>0,所以
>
,
因为函数y=lgx在定义域上递增,所以lg
>lg
,
即f(x1)>f(x2),
所以函数f(x)在定义域[-9,9]上单调递减.
| a-x |
| 10+x |
所以f(0)=lg
| a |
| 10 |
则a的值是10;
(2)由(1)得,f(x)=lg
| 10-x |
| 10+x |
函数f(x)在定义域上单调递减,证明如下:
任取x1,x2∈[-9,9],且x1<x2,
则
| 10-x1 |
| 10+x1 |
| 10-x2 |
| 10+x2 |
| (10-x1)(10+x2)-(10-x2)(10+x1) |
| (10+x1)(10+x2) |
=
| 20(x2-x1) |
| (10+x1)(10+x2) |
因为-9≤x1<x2≤9,所以x2-x1>0,
则
| 20(x2-x1) |
| (10+x1)(10+x2) |
| 10-x1 |
| 10+x1 |
| 10-x2 |
| 10+x2 |
因为函数y=lgx在定义域上递增,所以lg
| 10-x1 |
| 10+x1 |
| 10-x2 |
| 10+x2 |
即f(x1)>f(x2),
所以函数f(x)在定义域[-9,9]上单调递减.
点评:本题考查奇函数的性质,利用函数的单调性的定义证明函数的单调性,化简时需要注意应先比较真数的大小,才能得到f(x1)与f(x2)的大小,计算量大,属中档题.

练习册系列答案
相关题目
已知等差数列{an}的公差为2,若a1,a3,a4成等比数列,则a2的值为( )
| A、-4 | B、-10 | C、-8 | D、-6 |
若平面α⊥平面β,平面β⊥平面γ,则( )
| A、α∥γ | B、α⊥γ |
| C、α∥γ或α⊥γ | D、不确定 |
若l、m、n是互不相同的空间直线,α、β是不重合的平面,则下列结论正确的是( )
| A、α∥β,l?α,n?β⇒l∥n |
| B、α∥β,l?α⇒l⊥β |
| C、l⊥n,m⊥n⇒l∥m |
| D、l⊥α,l∥β⇒α⊥β |
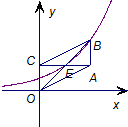 如图,面积为8的平行四边形OABC,对角线AC⊥OC,AC与BO交于点E,某指数函数y=ax(a>0,且a≠1)的图象经过点E,B,则a=( )
如图,面积为8的平行四边形OABC,对角线AC⊥OC,AC与BO交于点E,某指数函数y=ax(a>0,且a≠1)的图象经过点E,B,则a=( )