题目内容
已知等差数列{an}的公差为2,若a1,a3,a4成等比数列,则a2的值为( )
| A、-4 | B、-10 | C、-8 | D、-6 |
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:由等差数列中的三个数a1,a3,a4成等比数列求得数列首项,代入等差数列的通项公式求得a2的值.
解答:
解:由a1,a3,a4成等比数列,得a32=a1a4,
即(a1+4)2=a1(a1+6),解得:a1=-8.
∴a2=a1+d=-8+2=-6.
故选:D.
即(a1+4)2=a1(a1+6),解得:a1=-8.
∴a2=a1+d=-8+2=-6.
故选:D.
点评:本题考查了等差数列的通项公式,考查了等比数列的性质,是基础的计算题.

练习册系列答案
相关题目
已知全集U=R,集合A={x|x2-x-6≤0},B={x|
>0},那么集合A∩(∁UB)=( )
| x+1 |
| x-4 |
| A、{x|-2≤x<4} |
| B、{x|x≤3或x≥4} |
| C、{x|-2≤x<-1} |
| D、{x|-1≤x≤3} |
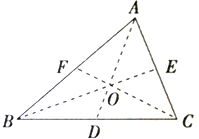 如图,在△ABC中,D、E、F分别是BC、CA、AB的中点,O是三角形内一点.求证:
如图,在△ABC中,D、E、F分别是BC、CA、AB的中点,O是三角形内一点.求证: