题目内容
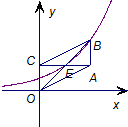如图，面积为8的平行四边形OABC，对角线AC⊥OC，AC与BO交于点E，某指数函数y=ax（a＞0，且a≠1）的图象经过点E，B，则a=（ ）A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
考点：指数函数的图像与性质
专题：函数的性质及应用
分析：首先设点E（t，at），则点B坐标为（2t，2at），又因为2at=a2t，所以at=2；然后根据平行四边形的面积是8，求出t的值，代入at=2，求出a的值即可．
解答：
解：设点E（t，at），则点B坐标为（2t，2at），
又因为2at=a2t，
所以at=2；
因为平行四边形OABC的面积S=OC×AC=at×2t=4t，又平行四边形OABC的面积为8
所以4t=8，t=2，
所以a2=2，
即a=
又因为2at=a2t，
所以at=2；
因为平行四边形OABC的面积S=OC×AC=at×2t=4t，又平行四边形OABC的面积为8
所以4t=8，t=2，
所以a2=2，
即a=
| 2 |
点评：本题主要考查了指数函数的图象和性质，属于基础题．
练习册系列答案
相关题目
已知集合A={1，2，3}，集合B={x∈Z|1＜x＜4}，则A∩B=（ ）
| A、{2，3} |
| B、{1，4} |
| C、{1，2，3，4} |
| D、∅ |