题目内容
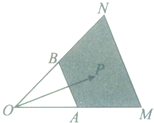 如图
如图| OM |
| OA |
| ON |
| OB |
| OP |
| OP |
| ON |
| OM |
(1)若P在线段AB上,则x+y=
(2)若P在阴影部分内(含边界)则x+y的取值范围是
考点:平面向量的基本定理及其意义
专题:计算题,平面向量及应用
分析:(1)若P在线段AB上,设
=λ
,则有
=
,由于
=x
+y
,
=2
,
=2
,
则有2x+2y=1,即可得到x+y;
(2)考虑两端,即P在线段AB上,则x+y=
,P落在线段MN上,则x+y=1.即可得到取值范围.
| BP |
| PA |
| OP |
| ||||
| 1+λ |
| OP |
| ON |
| OM |
| ON |
| OB |
| OM |
| OA |
则有2x+2y=1,即可得到x+y;
(2)考虑两端,即P在线段AB上,则x+y=
| 1 |
| 2 |
解答:
解:(1)若P在线段AB上,设
=λ
,
则有
=
,
由于
=x
+y
,
=2
,
=2
,
则
=2x
+2y
,
即有2x=
,2y=
,
则有2x+2y=1,则x+y=
;
(2)若P在阴影部分内(含边界),
则若P在线段AB上,则x+y=
,
若P落在线段MN上,则x+y=1.
则P落在阴影内,则有
<x+y<1.
故x+y的取值范围是[
,1],
故答案为:
,[
,1].
| BP |
| PA |
则有
| OP |
| ||||
| 1+λ |
由于
| OP |
| ON |
| OM |
| ON |
| OB |
| OM |
| OA |
则
| OP |
| OB |
| OA |
即有2x=
| 1 |
| 1+λ |
| λ |
| 1+λ |
则有2x+2y=1,则x+y=
| 1 |
| 2 |
(2)若P在阴影部分内(含边界),
则若P在线段AB上,则x+y=
| 1 |
| 2 |
若P落在线段MN上,则x+y=1.
则P落在阴影内,则有
| 1 |
| 2 |
故x+y的取值范围是[
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查三角形法则,是一个基础题,向量是数形结合的最好的工具,在解题时注意发挥向量的优点.

练习册系列答案
相关题目
命题“?x0∈R,2 x0≤0”的否定为( )
| A、?x∈R,2x≤0 |
| B、?x∈R,2x≥0 |
| C、?x∈R,2x<0 |
| D、?x∈R,2x>0 |
如图中的直线l1、l2、l3的斜率分别为k1、k2、k3,则( )
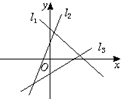

| A、k1<k2<k3 |
| B、k3<k1<k2 |
| C、k3<k2<k1 |
| D、k1<k3<k2 |
10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有( )
| A、a>b>c |
| B、b>c>a |
| C、c>a>b |
| D、c>b>a |