题目内容
函数f（x）=2-x的图象与函数g（x）=
的图象相交于A、B两点，则|AB|= ．
| 2x-x2 |
考点：函数的图象
专题：函数的性质及应用
分析：把两函数图象交点问题，转化为方程组的解的问题．
解答：
解：联立方程
，解得x=1或2，
即A（1，1），B（2，0）．
所以，|AB|=
．
故答案为：
． 
|
即A（1，1），B（2，0）．
所以，|AB|=
| 2 |
故答案为：
| 2 |
点评：本题考查函数图象交点问题，属基础题，这类问题可考虑从数的角度（解方程组）或形的角度（函数图象）进行求解．
练习册系列答案
相关题目
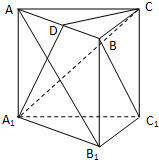如图，已知直三棱柱ABC-A1B1C1中，AC⊥BC，D为AB的中点，AC=BC=BB1．
如图，D为△ABC的边BC中点，E在AC上且AE=3，EC=2，AD交BE于F，那么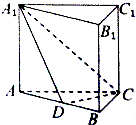
如图，三棱柱ABC-A1B1C1中，底面是边长为2的正三角形，侧棱AA1⊥底面ABC，D为AB的中点，且A1D与底面ABC所成角的正切值为2，则三棱锥A1-ACD外接球的表面积为已知实数x，y满足：
，则z=2|x|+y的取值范围是（ ）
|
| A、[0，11] |
| B、[-5，11] |
| C、[-1，11] |
| D、[1，11] |