题目内容
12.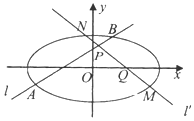 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,过$P({0,\frac{b}{2}})$的直线l与椭圆交于A,B两点,过Q(x0,0)(|x0|<a)的直线l'与椭圆交于M,N两点.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,过$P({0,\frac{b}{2}})$的直线l与椭圆交于A,B两点,过Q(x0,0)(|x0|<a)的直线l'与椭圆交于M,N两点.(1)当l的斜率是k时,用a,b,k表示出|PA|•|PB|的值;
(2)若直线l,l'的倾斜角互补,是否存在实数x0,使$\frac{{|{PA}|•|{PB}|}}{{{{|{MN}|}^2}}}$为定值,若存在,求出该定值及x0,若不存在,说明理由.
分析 (1)由题意可知:椭圆的焦点在x轴上,设直线AB的方程:$y=kx+\frac{b}{2},A({{x_1}{y_1}}),B({{x_2},{y_2}})$,代入椭圆方程,由韦达定理${x_1}{x_2}=\frac{{-3{a^2}{b^2}}}{{4({{a^2}{k^2}+{b^2}})}}$,因此,由弦长公式可知:$|{PA}|•|{PB}|=\sqrt{1+{k^2}}|{x_1}|•\sqrt{1+{k^2}}|{x_2}|=({1+{k^2}})|{{x_1}{x_2}}|=\frac{{3{a^2}{b^2}({1+{k^2}})}}{{4({{a^2}{k^2}+{b^2}})}}$,
(2)当直线MN的斜率存在时:设直线MN的方程:y=-k(x-x0),代入椭圆方程,由韦达定理可知:${x_3}+{x_4}=\frac{{2{a^2}{k^2}{x_0}}}{{{a^2}{k^2}+{b^2}}},{x_3}{x_4}=\frac{{{a^2}{k^2}x_0^2-{a^2}{b^2}}}{{{a^2}{k^2}+{b^2}}}$,由弦长公式求得丨MN丨,则${|{MN}|^2}=({1+{k^2}})•\frac{{4({{a^2}b+{a^4}{b^2}{k^2}-{a^2}{b^2}{k^2}x_0^2})}}{{{{({{a^2}{k^2}+{b^2}})}^2}}}$,$\frac{{|{PA}|•|{PB}|}}{{{{|{MN}|}^2}}}=\frac{3}{16}•\frac{{{a^2}{b^2}({{b^2}+{a^2}{k^2}})}}{{{a^2}{b^4}+{a^4}{b^2}{k^2}-{a^2}{b^2}{k^2}x_0^2}}=\frac{3}{16}•\frac{{{b^2}+{a^2}{k^2}}}{{{b^2}+{a^2}{k^2}-{k^2}x_0^2}}$,当x0=0时,$\frac{{|{PA}|•|{PB}|}}{{{{|{MN}|}^2}}}=\frac{3}{16}$为常数,当直线MN的斜率不存在时:$\frac{{|{PA}|•|{PB}|}}{{{{|{MN}|}^2}}}=\frac{{\frac{{3{b^2}}}{4}}}{{4{b^2}-\frac{{4{b^2}}}{a^2}x_0^2}},{x_0}=0$时,$\frac{{|{PA}|•|{PB}|}}{{{{|{MN}|}^2}}}=\frac{3}{16}$为定值,所以当x0=0时,$\frac{{|{PA}|•|{PB}|}}{{{{|{MN}|}^2}}}=\frac{3}{16}$为常数.
解答 解:(1)椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,焦点在x轴上,焦距为2c,
设直线AB的方程:$y=kx+\frac{b}{2},A({{x_1}{y_1}}),B({{x_2},{y_2}})$,
由$\left\{{\begin{array}{l}{y=kx+\frac{b}{2}}\\{{b^2}{x^2}+{a^2}{y^2}={a^2}{b^2}}\end{array}}\right.$,整理得:$({{a^2}{k^2}+{b^2}}){x^2}+{a^2}bkx-\frac{{3{a^2}{b^2}}}{4}=0$,
由韦达定理可知:${x_1}{x_2}=\frac{{-3{a^2}{b^2}}}{{4({{a^2}{k^2}+{b^2}})}}$,…(3分)
$|{PA}|•|{PB}|=\sqrt{1+{k^2}}|{x_1}|•\sqrt{1+{k^2}}|{x_2}|=({1+{k^2}})|{{x_1}{x_2}}|=\frac{{3{a^2}{b^2}({1+{k^2}})}}{{4({{a^2}{k^2}+{b^2}})}}$,…(6分)
(2)当直线MN的斜率存在时:设直线MN的方程:y=-k(x-x0),M(x3,y3),N(x4,y4).
由$\left\{{\begin{array}{l}{y=-k({x-{x_0}})}\\{{b^2}{x^2}+{a^2}{y^2}={a^2}{b^2}}\end{array}}\right.$,可知得:$({{a^2}{k^2}+{b^2}}){x^2}-2{a^2}{k^2}{x_0}x+{a^2}{k^2}x_0^2-{a^2}{b^2}=0$,
则$△=4({{a^2}{b^2}+{a^4}{b^2}{k^2}-{a^2}{b^2}{k^2}x_0^2})>0$,
由韦达定理可知:${x_3}+{x_4}=\frac{{2{a^2}{k^2}{x_0}}}{{{a^2}{k^2}+{b^2}}},{x_3}{x_4}=\frac{{{a^2}{k^2}x_0^2-{a^2}{b^2}}}{{{a^2}{k^2}+{b^2}}}$,
由弦长公式可知:丨MN丨=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{3}+{x}_{4})^{2}-4{x}_{3}{x}_{4}}$,…(8分)
∴${|{MN}|^2}=({1+{k^2}})•\frac{{4({{a^2}b+{a^4}{b^2}{k^2}-{a^2}{b^2}{k^2}x_0^2})}}{{{{({{a^2}{k^2}+{b^2}})}^2}}}$,…(10分)
$\frac{{|{PA}|•|{PB}|}}{{{{|{MN}|}^2}}}=\frac{3}{16}•\frac{{{a^2}{b^2}({{b^2}+{a^2}{k^2}})}}{{{a^2}{b^4}+{a^4}{b^2}{k^2}-{a^2}{b^2}{k^2}x_0^2}}=\frac{3}{16}•\frac{{{b^2}+{a^2}{k^2}}}{{{b^2}+{a^2}{k^2}-{k^2}x_0^2}}$,…(13分)
∴当x0=0时,$\frac{{|{PA}|•|{PB}|}}{{{{|{MN}|}^2}}}=\frac{3}{16}$为常数…(14分)
当直线MN的斜率不存在时:$\frac{{|{PA}|•|{PB}|}}{{{{|{MN}|}^2}}}=\frac{{\frac{{3{b^2}}}{4}}}{{4{b^2}-\frac{{4{b^2}}}{a^2}x_0^2}},{x_0}=0$时,
$\frac{{|{PA}|•|{PB}|}}{{{{|{MN}|}^2}}}=\frac{3}{16}$为定值.
综上:所以当x0=0时,$\frac{{|{PA}|•|{PB}|}}{{{{|{MN}|}^2}}}=\frac{3}{16}$为常数.…(15分)
点评 本题考查直线与椭圆位置关系的综合应用,考查弦长公式,韦达定理在求直线与椭圆的位置关系中的应用,考查计算能力,计算量大,综合性强,属于难题.

| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 3 | D. | -3 |
(Ⅰ)求曲线y=f(x);
(Ⅱ) 设g(x)=f'(x)e-x,求函数g(x)的极值.
| A. | 向右平移$\frac{5π}{6}$个单位 | B. | 向右平移$\frac{5π}{12}$个单位 | ||
| C. | 向左平移$\frac{5π}{6}$个单位 | D. | 向左平移$\frac{5π}{12}$个单位 |
| A. | $\frac{1}{24}$ | B. | $\frac{1}{19}$ | C. | $\frac{1}{11}$ | D. | $-\frac{23}{8}$ |
| A. | (-3,3) | B. | (-3,1) | C. | (-3,0)∪(0,3) | D. | (-1,0)∪(0,1) |
| A. | (-∞,2)∪(1,+∞) | B. | (-2,1) | C. | (-∞,-1)∪(2,+∞) | D. | (-1,2) |
| A. | f(a)<f(c)<f(b) | B. | f(c)<f(b)<f(a) | C. | f(a)<f(b)<f(c) | D. | f(b)<f(c)<f(a) |