题目内容
7.袋中有大小相同的3个红球,2个白球,1个黑球.若不放回摸球,每次1球,摸取3次,则恰有两次红球的概率为$\frac{9}{20}$;若有放回摸球,每次1球,摸取3次,则摸到红球次数的期望为$\frac{3}{2}$.分析 ①每次1球,摸取3次,则恰有两次红球的概率=$\frac{{∁}_{3}^{2}{∁}_{3}^{1}}{{∁}_{6}^{3}}$.
②设摸到红球次数为X,则X的取值分别为0,1,2,3,P(X=k)=$\frac{{∁}_{3}^{k}{∁}_{3}^{3-k}}{{∁}_{6}^{3}}$,(k=0,1,2,3).
解答 解:①每次1球,摸取3次,则恰有两次红球的概率P=$\frac{{∁}_{3}^{2}{∁}_{3}^{1}}{{∁}_{6}^{3}}$=$\frac{3×3}{\frac{6×5×4}{1×2×3}}$=$\frac{9}{20}$.
②设摸到红球次数为X,则X的可能取值为0,1,2,3,P(X=k)=$\frac{{∁}_{3}^{k}{∁}_{3}^{3-k}}{{∁}_{6}^{3}}$,(k=0,1,2,3).
∴P(X=0)=$\frac{1}{20}$,P(X=1)=$\frac{9}{20}$,P(X=2)=$\frac{9}{20}$,P(X=3)=$\frac{1}{20}$,
∴E(X)=0+1×$\frac{9}{20}$+2×$\frac{9}{20}$+3×$\frac{1}{20}$=$\frac{3}{2}$.
故答案为:$\frac{9}{20},\frac{3}{2}$.
点评 本题考查了超几何分布列的概率计算公式及其数学期望,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
18.已知不等式组$\left\{\begin{array}{l}{2x+y-3≤0}\\{x-y+2≥0}\\{2x-3y-3≤0}\end{array}\right.$表示的平面区域为D,P(x,y)为D上一点,则|x+4|+|y+3|的最大值为( )
| A. | $\frac{17}{2}$ | B. | 9 | C. | $\frac{29}{3}$ | D. | 10 |
2.设x,y满足约束条件$\left\{{\begin{array}{l}{x+y≤3}\\{x-y≥-1}\\{y≥1}\end{array}}\right.$若0≤ax+by≤2恒成立,则a2+b2的最大值是( )
| A. | 1 | B. | $\frac{8}{9}$ | C. | $\frac{20}{9}$ | D. | 4 |
16.已知命题$p:sinx=\frac{1}{2}$,命题$q:x=\frac{π}{6}+2kπ,k∈Z$,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
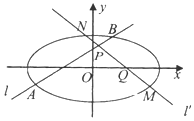 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,过$P({0,\frac{b}{2}})$的直线l与椭圆交于A,B两点,过Q(x0,0)(|x0|<a)的直线l'与椭圆交于M,N两点.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,过$P({0,\frac{b}{2}})$的直线l与椭圆交于A,B两点,过Q(x0,0)(|x0|<a)的直线l'与椭圆交于M,N两点.