题目内容
2．函数f（x）=aex-1-$\sqrt{x}$+1的图象在点（1，f（1））处的切线斜率为$\frac{5}{2}$，则实数a=（ ）| A． | $\frac{1}{2}$ | B． | $-\frac{1}{2}$ | C． | 3 | D． | -3 |
分析 求导数，利用函数f（x）=aex-1-$\sqrt{x}$+1的图象在点（1，f（1））处的切线斜率为$\frac{5}{2}$，建立方程，即可求出a的值．
解答 解：由题意，求导得：f′（x）=aex-1-$\frac{1}{2\sqrt{x}}$，
因为函数f（x）=aex-1-$\sqrt{x}$+1的图象在点（1，f（1））处的切线斜率为$\frac{5}{2}$，
所以f′（1）=a-$\frac{1}{2}$=$\frac{5}{2}$，即a=3，
故选C．
点评 此题考查学生会利用导数求曲线上过某点切线方程的斜率，是一道基础题．
练习册系列答案
应用题作业本系列答案
相关题目
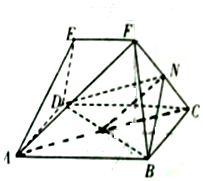如图，在多面体ABCDEF中，四边形ABCD为矩形，△ADE，△BCF均为等边三角形，EF∥AB，EF=AD=$\frac{1}{2}$AB，N为线段PC的中点．
7．已知数列{an}为等差数列，a1+a2+a3=3，a5+a6+a7=9，则a10=（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
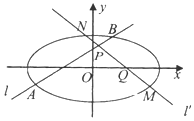已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$，过$P（{0，\frac{b}{2}}）$的直线l与椭圆交于A，B两点，过Q（x0，0）（|x0|＜a）的直线l'与椭圆交于M，N两点．