题目内容
1.已知f(x)的定义域是(0,+∞),f'(x)为f(x)的导函数,且满足f(x)<f'(x),则不等式${e^{-x}}f({{x^2}+x})>{e^{{x^2}-2}}$f(2)的解集是( )| A. | (-∞,2)∪(1,+∞) | B. | (-2,1) | C. | (-∞,-1)∪(2,+∞) | D. | (-1,2) |
分析 构造新函数g(x)=$\frac{f(x)}{x}$,通过求导得到g(x)的单调性,所解的不等式转化为求g(x2+x)>g(2),结合函数的单调性得到不等式,求解得答案.
解答 解:设g(x)=$\frac{f(x)}{{e}^{x}}$,(x>0),
∵f(x)<f'(x),∴g′(x)=$\frac{f′(x)-f(x)}{{e}^{x}}$>0,
∴g(x)在(0,+∞)单调递增,
由${e^{-x}}f({{x^2}+x})>{e^{{x^2}-2}}$f(2),得$\frac{f({x}^{2}+x)}{{e}^{{x}^{2}+x}}>\frac{f(2)}{{e}^{2}}$,即g(x2+x)>g(2),
∴x2+x>2,
解得:x<-2或x>1.
∴不等式${e^{-x}}f({{x^2}+x})>{e^{{x^2}-2}}$f(2)的解集是(-∞,-2)∪(1,+∞).
故选:A.
点评 本题考查了函数的单调性问题,考查导数的应用,构造新函数g(x)是解题的关键,是中档题.

练习册系列答案
相关题目
16.已知命题$p:sinx=\frac{1}{2}$,命题$q:x=\frac{π}{6}+2kπ,k∈Z$,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
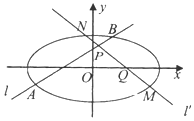 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,过$P({0,\frac{b}{2}})$的直线l与椭圆交于A,B两点,过Q(x0,0)(|x0|<a)的直线l'与椭圆交于M,N两点.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,过$P({0,\frac{b}{2}})$的直线l与椭圆交于A,B两点,过Q(x0,0)(|x0|<a)的直线l'与椭圆交于M,N两点.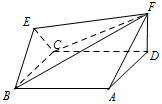 如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且$FD=\sqrt{3}$.
如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且$FD=\sqrt{3}$.